Lagrangian Neural Networks for Reversible Dissipative Evolution

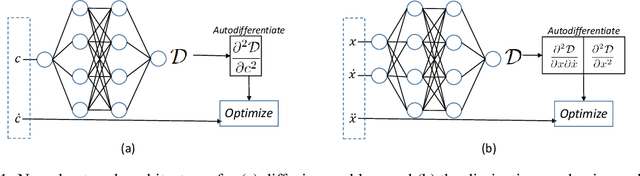
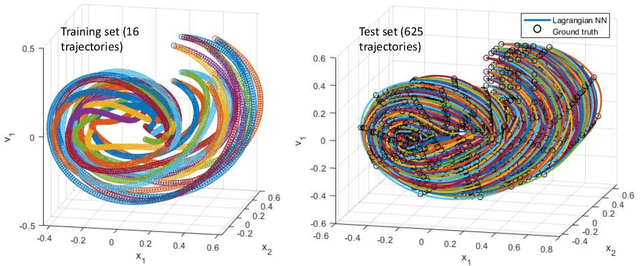
There is a growing attention given to utilizing Lagrangian and Hamiltonian mechanics with network training in order to incorporate physics into the network. Most commonly, conservative systems are modeled, in which there are no frictional losses, so the system may be run forward and backward in time without requiring regularization. This work addresses systems in which the reverse direction is ill-posed because of the dissipation that occurs in forward evolution. The novelty is the use of Morse-Feshbach Lagrangian, which models dissipative dynamics by doubling the number of dimensions of the system in order to create a mirror latent representation that would counterbalance the dissipation of the observable system, making it a conservative system, albeit embedded in a larger space. We start with their formal approach by redefining a new Dissipative Lagrangian, such that the unknown matrices in the Euler-Lagrange's equations arise as partial derivatives of the Lagrangian with respect to only the observables. We then train a network from simulated training data for dissipative systems such as Fickian diffusion that arise in materials sciences. It is shown by experiments that the systems can be evolved in both forward and reverse directions without regularization beyond that provided by the Morse-Feshbach Lagrangian. Experiments of dissipative systems, such as Fickian diffusion, demonstrate the degree to which dynamics can be reversed.

Towards Microstructural State Variables in Materials Systems

The vast combination of material properties seen in nature are achieved by the complexity of the material microstructure. Advanced characterization and physics based simulation techniques have led to generation of extremely large microstructural datasets. There is a need for machine learning techniques that can manage data complexity by capturing the maximal amount of information about the microstructure using the least number of variables. This paper aims to formulate dimensionality and state variable estimation techniques focused on reducing microstructural image data. It is shown that local dimensionality estimation based on nearest neighbors tend to give consistent dimension estimates for natural images for all p-Minkowski distances. However, it is found that dimensionality estimates have a systematic error for low-bit depth microstructural images. The use of Manhattan distance to alleviate this issue is demonstrated. It is also shown that stacked autoencoders can reconstruct the generator space of high dimensional microstructural data and provide a sparse set of state variables to fully describe the variability in material microstructures.