Bayesian Causal Inference

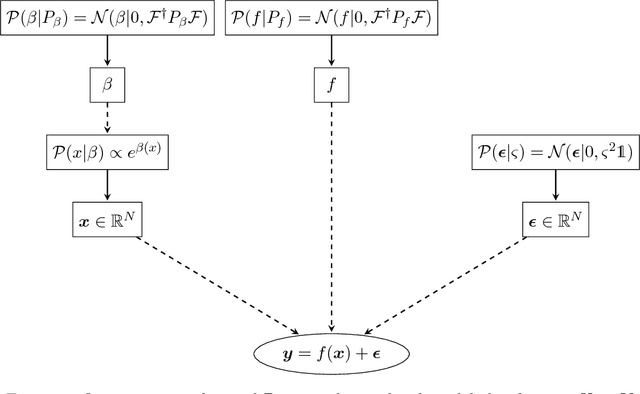
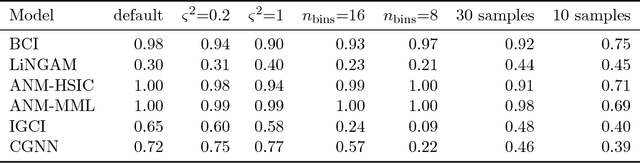
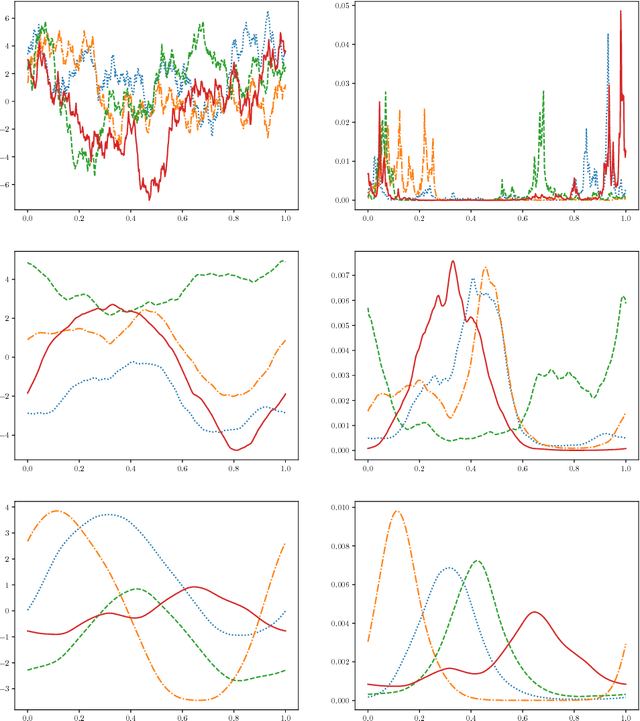
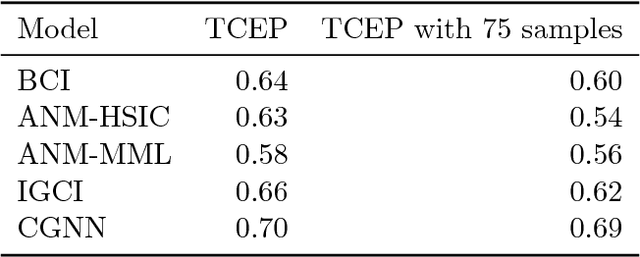
We address the problem of two-variable causal inference. This task is to infer an existing causal relation between two random variables, i.e. $X \rightarrow Y$ or $Y \rightarrow X$, from purely observational data. We briefly review a number of state-of-the-art methods for this, including very recent ones. A novel inference method is introduced, Bayesian Causal Inference (BCI), which assumes a generative Bayesian hierarchical model to pursue the strategy of Bayesian model selection. In the model the distribution of the cause variable is given by a Poisson lognormal distribution, which allows to explicitly regard discretization effects. We assume Fourier diagonal Field covariance operators. The generative model assumed provides synthetic causal data for benchmarking our model in comparison to existing State-of-the-art models, namely LiNGAM, ANM-HSIC, ANM-MML, IGCI and CGNN. We explore how well the above methods perform in case of high noise settings, strongly discretized data and very sparse data. BCI performs generally reliable with synthetic data as well as with the real world TCEP benchmark set, with an accuracy comparable to state-of-the-art algorithms.