Geometry of the Hough transforms with applications to synthetic data

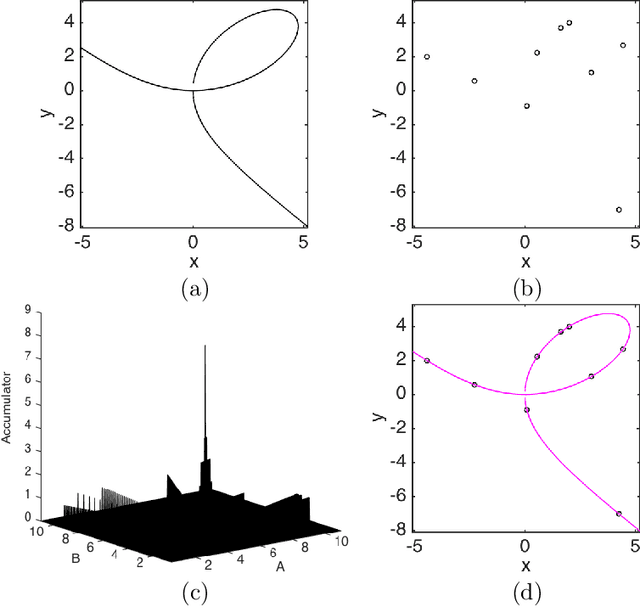
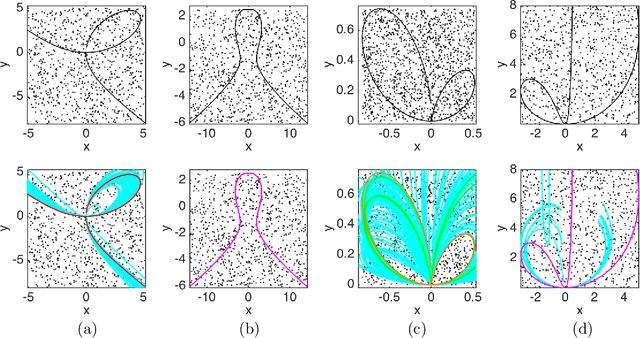
In the framework of the Hough transform technique to detect curves in images, we provide a bound for the number of Hough transforms to be considered for a successful optimization of the accumulator function in the recognition algorithm. Such a bound is consequence of geometrical arguments. We also show the robustness of the results when applied to synthetic datasets strongly perturbed by noise. An algebraic approach, discussed in the appendix, leads to a better bound of theoretical interest in the exact case.

An iterative approach to Hough transform without re-voting

Many bone shapes in the human skeleton are characterized by profiles that can be associated to equations of algebraic curves. Fixing the parameters in the curve equation, by means of a classical pattern recognition procedure like the Hough transform technique, it is then possible to associate an equation to a specific bone profile. However, most skeleton districts are more accurately described by piecewise defined curves. This paper utilizes an iterative approach of the Hough transform without re-voting, to provide an efficient procedure for describing the profile of a bone in the human skeleton as a collection of different but continuously attached curves.