Quantifying the Impact of Parameter Tuning on Nature-Inspired Algorithms

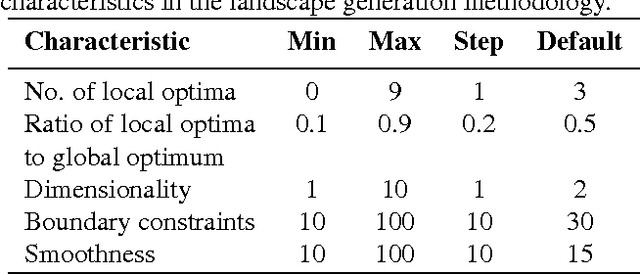
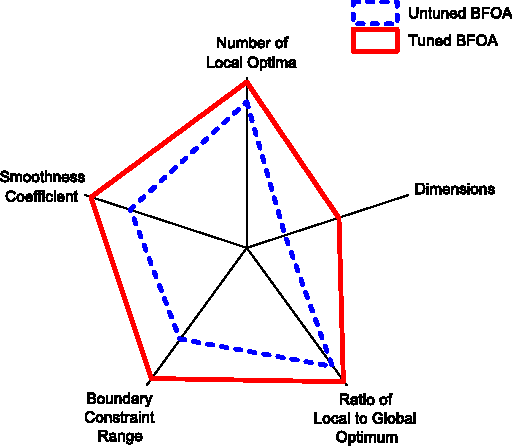
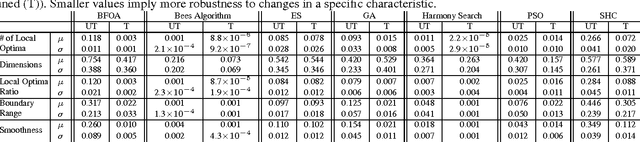
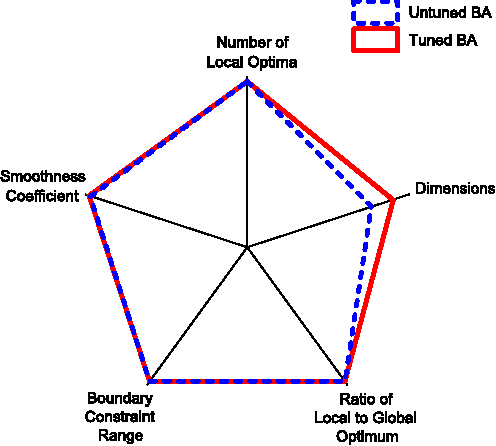
The problem of parameterization is often central to the effective deployment of nature-inspired algorithms. However, finding the optimal set of parameter values for a combination of problem instance and solution method is highly challenging, and few concrete guidelines exist on how and when such tuning may be performed. Previous work tends to either focus on a specific algorithm or use benchmark problems, and both of these restrictions limit the applicability of any findings. Here, we examine a number of different algorithms, and study them in a "problem agnostic" fashion (i.e., one that is not tied to specific instances) by considering their performance on fitness landscapes with varying characteristics. Using this approach, we make a number of observations on which algorithms may (or may not) benefit from tuning, and in which specific circumstances.

Fitness Landscape-Based Characterisation of Nature-Inspired Algorithms

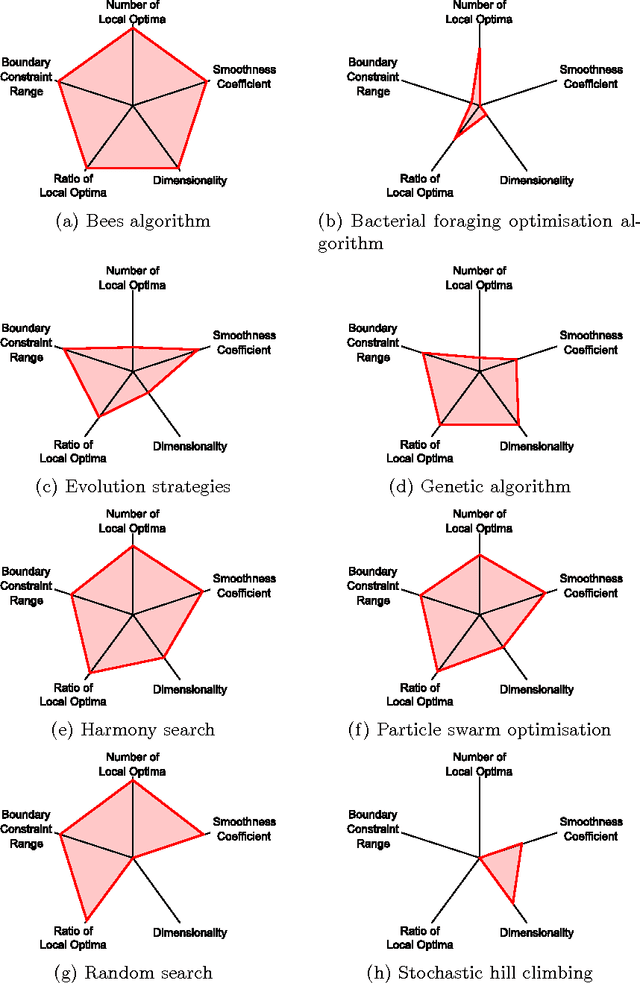
A significant challenge in nature-inspired algorithmics is the identification of specific characteristics of problems that make them harder (or easier) to solve using specific methods. The hope is that, by identifying these characteristics, we may more easily predict which algorithms are best-suited to problems sharing certain features. Here, we approach this problem using fitness landscape analysis. Techniques already exist for measuring the "difficulty" of specific landscapes, but these are often designed solely with evolutionary algorithms in mind, and are generally specific to discrete optimisation. In this paper we develop an approach for comparing a wide range of continuous optimisation algorithms. Using a fitness landscape generation technique, we compare six different nature-inspired algorithms and identify which methods perform best on landscapes exhibiting specific features.