Matan Ben-Dov
Regularized second-order optimization of tensor-network Born machines
Jan 30, 2025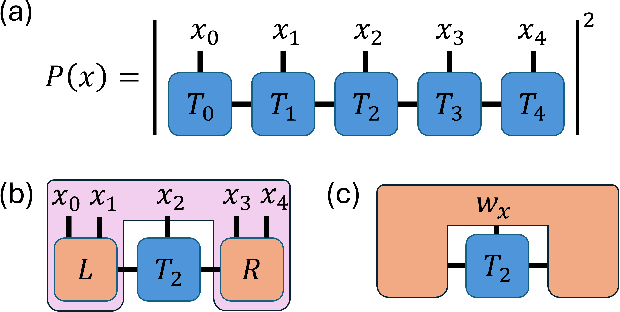
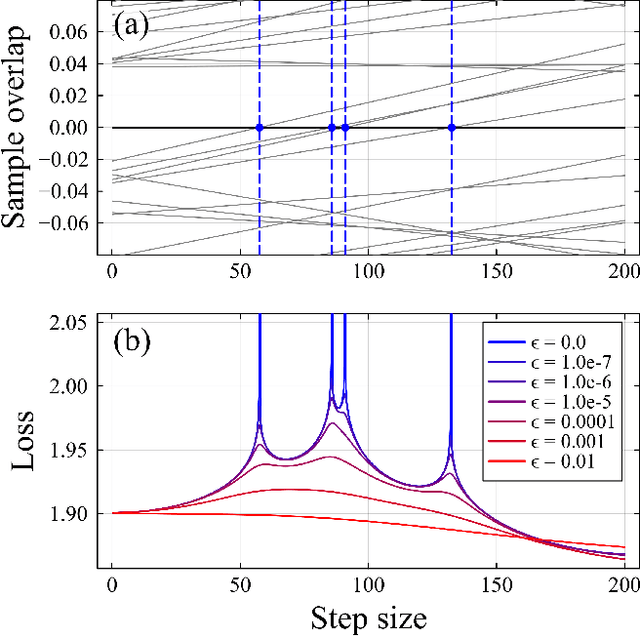
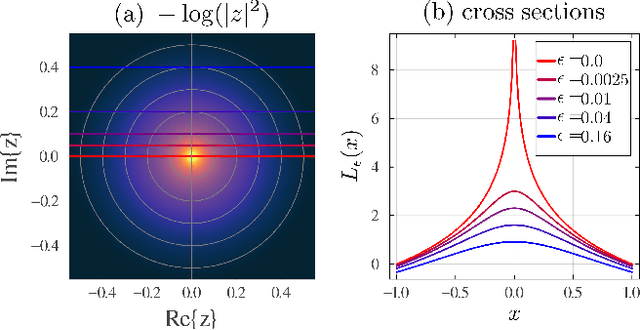
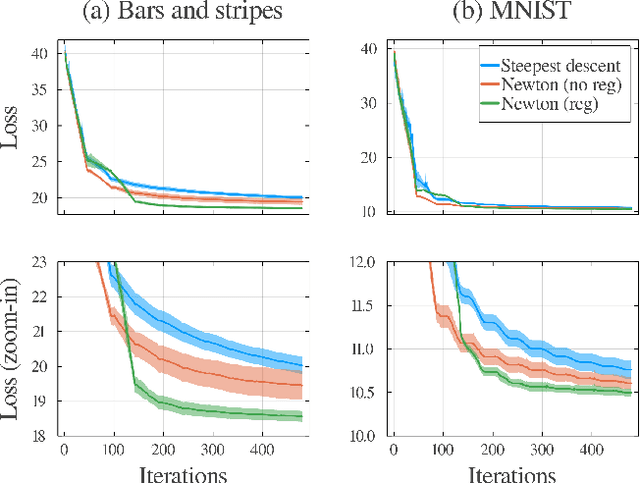
Abstract:Tensor-network Born machines (TNBMs) are quantum-inspired generative models for learning data distributions. Using tensor-network contraction and optimization techniques, the model learns an efficient representation of the target distribution, capable of capturing complex correlations with a compact parameterization. Despite their promise, the optimization of TNBMs presents several challenges. A key bottleneck of TNBMs is the logarithmic nature of the loss function that is commonly used for this problem. The single-tensor logarithmic optimization problem cannot be solved analytically, necessitating an iterative approach that slows down convergence and increases the risk of getting trapped in one of many non-optimal local minima. In this paper, we present an improved second-order optimization technique for TNBM training, which significantly enhances convergence rates and the quality of the optimized model. Our method employs a modified Newton's method on the manifold of normalized states, incorporating regularization of the loss landscape to mitigate local minima issues. We demonstrate the effectiveness of our approach by training a one-dimensional matrix product state (MPS) on both discrete and continuous datasets, showcasing its advantages in terms of stability, efficiency, and generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge