Maria del Mar Gonzalez
Universidad Autonoma de Madrid
Deterministic Decoupling of Global Features and its Application to Data Analysis
Jul 05, 2022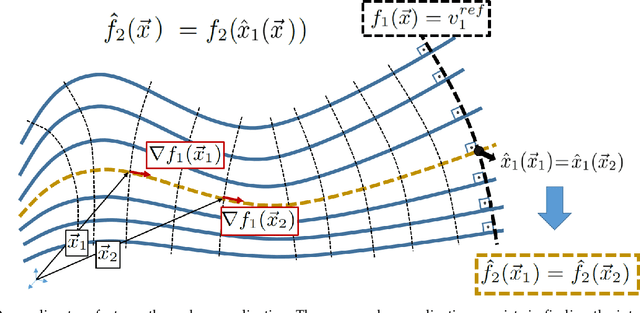
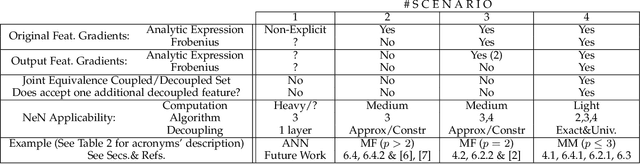
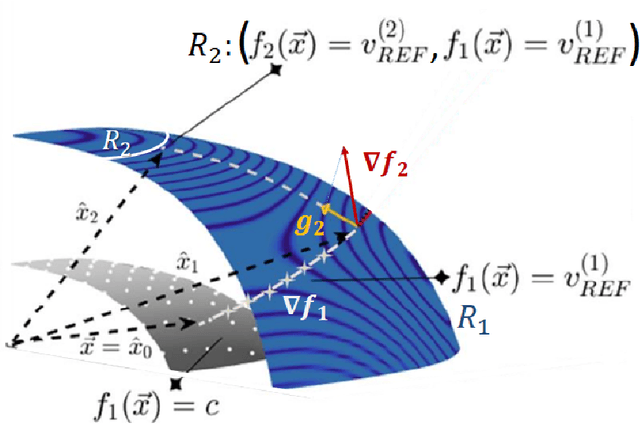
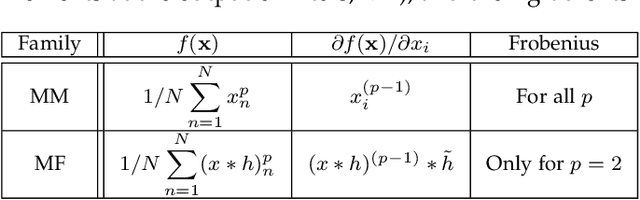
Abstract:We introduce a method for deterministic decoupling of global features and show its applicability to improve data analysis performance, as well as to open new venues for feature transfer. We propose a new formalism that is based on defining transformations on submanifolds, by following trajectories along the features gradients. Through these transformations we define a normalization that, we demonstrate, allows for decoupling differentiable features. By applying this to sampling moments, we obtain a quasi-analytic solution for the orthokurtosis, a normalized version of the kurtosis that is not just decoupled from mean and variance, but also from skewness. We apply this method in the original data domain and at the output of a filter bank to regression and classification problems based on global descriptors, obtaining a consistent and significant improvement in performance as compared to using classical (non-decoupled) descriptors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge