Input-driven circuit reconfiguration in critical recurrent neural networks

Changing a circuit dynamically, without actually changing the hardware itself, is called reconfiguration, and is of great importance due to its manifold technological applications. Circuit reconfiguration appears to be a feature of the cerebral cortex, and hence understanding the neuroarchitectural and dynamical features underlying self-reconfiguration may prove key to elucidate brain function. We present a very simple single-layer recurrent network, whose signal pathways can be reconfigured "on the fly" using only its inputs, with no changes to its synaptic weights. We use the low spatio-temporal frequencies of the input to landscape the ongoing activity, which in turn permits or denies the propagation of traveling waves. This mechanism uses the inherent properties of dynamically-critical systems, which we guarantee through unitary convolution kernels. We show this network solves the classical connectedness problem, by allowing signal propagation only along the regions to be evaluated for connectedness and forbidding it elsewhere.

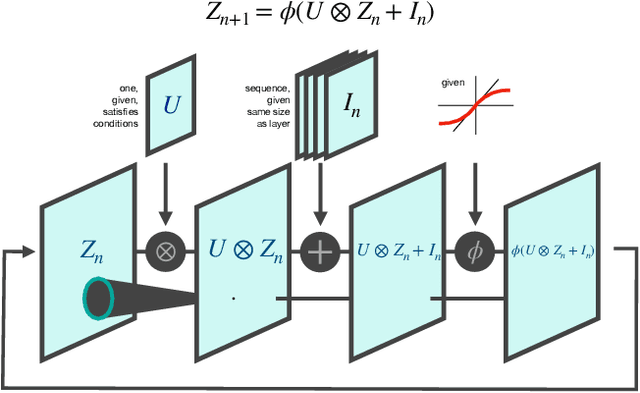
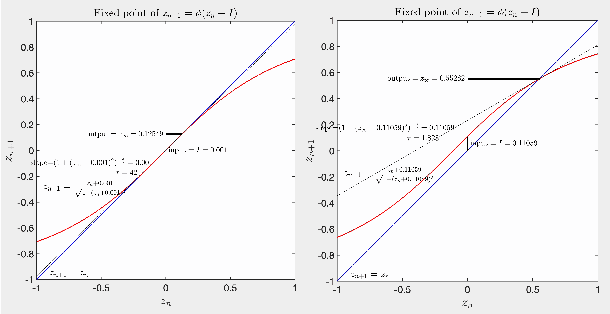
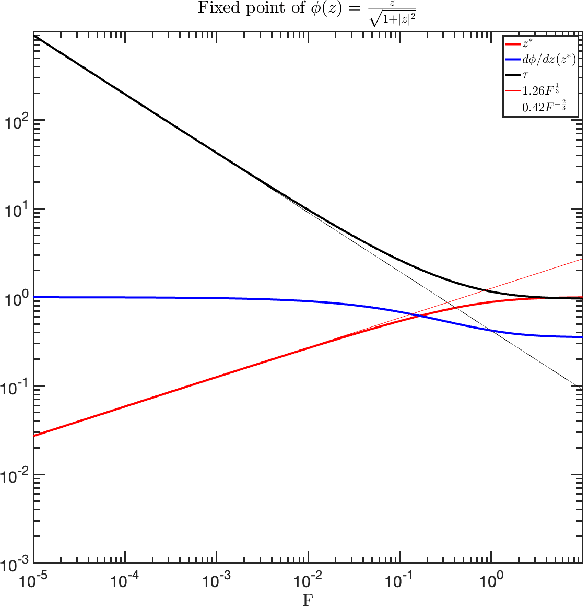
On the dynamics of convolutional recurrent neural networks near their critical point

We examine the dynamical properties of a single-layer convolutional recurrent network with a smooth sigmoidal activation function, for small values of the inputs and when the convolution kernel is unitary, so all eigenvalues lie exactly at the unit circle. Such networks have a variety of hallmark properties: the outputs depend on the inputs via compressive nonlinearities such as cubic roots, and both the timescales of relaxation and the length-scales of signal propagation depend sensitively on the inputs as power laws, both diverging as the input to 0. The basic dynamical mechanism is that inputs to the network generate ongoing activity, which in turn controls how additional inputs or signals propagate spatially or attenuate in time. We present analytical solutions for the steady states when the network is forced with a single oscillation and when a background value creates a steady state of ongoing activity, and derive the relationships shaping the value of the temporal decay and spatial propagation length as a function of this background value.

Convolutional unitary or orthogonal recurrent neural networks

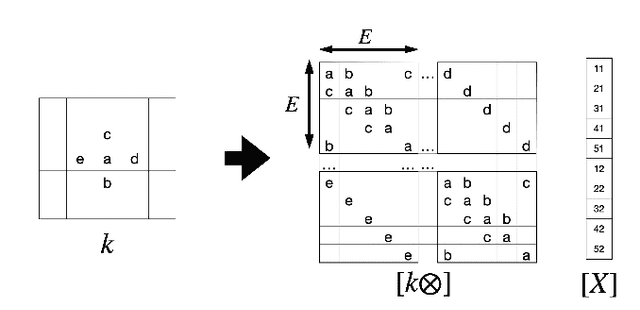
Recurrent neural networks are extremely powerful yet hard to train. One of their issues is the vanishing gradient problem, whereby propagation of training signals may be exponentially attenuated, freezing training. Use of orthogonal or unitary matrices, whose powers neither explode nor decay, has been proposed to mitigate this issue, but their computational expense has hindered their use. Here we show that in the specific case of convolutional RNNs, we can define a convolutional exponential and that this operation transforms antisymmetric or anti-Hermitian convolution kernels into orthogonal or unitary convolution kernels. We explicitly derive FFT-based algorithms to compute the kernels and their derivatives. The computational complexity of parametrizing this subspace of orthogonal transformations is thus the same as the networks' iteration.