Mahtab Uddin
Riccati-based feedback stabilization for unstable Power system models
Jun 26, 2020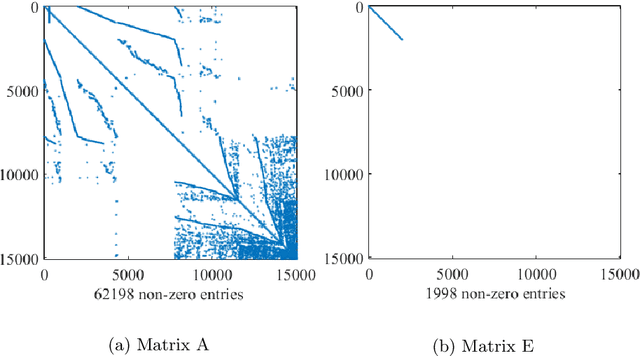
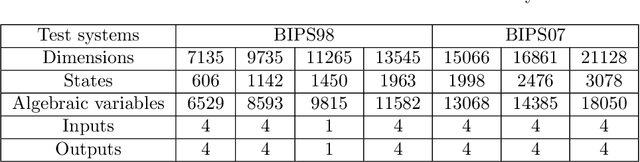
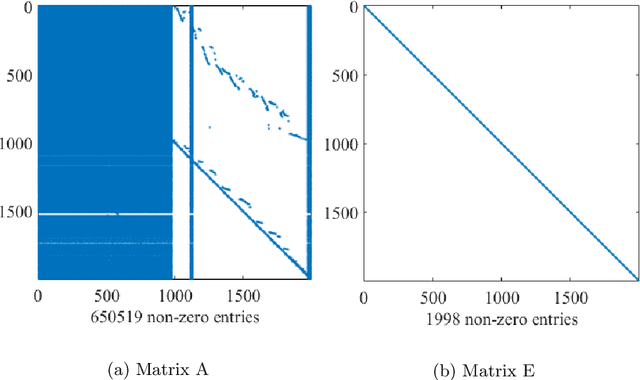
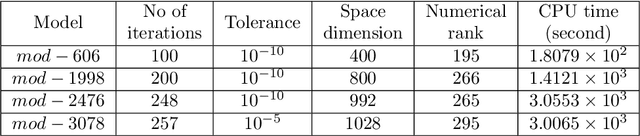
Abstract:In this article, the objective is mainly focused on finding optimal control for the large-scale sparse unstable power system models using optimal feedback matrix achieved by the Riccati-based feedback stabilization process. Our aim is to solve the Continuous-time Algebraic Riccati Equations (CAREs) governed from large-scale unstable power system models, which are of index-1 descriptor systems with a sparse pattern. We propose the projection-based Rational Krylov Subspace Method (RKSM) for the computation of the solution of the CAREs, the novelties of RKSM are sparsity-preserving techniques and the implementation of time convenient recursive adaptive shift parameters. We modify the machine-independent Alternating Direction Implicit (ADI) technique based nested iterative Kleinman-Newton (KN) method and adjust this to solve the CAREs governed from large-scale sparse unstable power system models. We compare the results achieved by the Kleinman-Newton method with that of using the RKSM. The applicability and adaptability of the proposed methods are justified through the Brazilian Inter-Connected Power System (BIPS) models and their transient behaviors are comparatively analyzed by both tabular and graphical approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge