Optimal active particle navigation meets machine learning

The question of how "smart" active agents, like insects, microorganisms, or future colloidal robots need to steer to optimally reach or discover a target, such as an odor source, food, or a cancer cell in a complex environment has recently attracted great interest. Here, we provide an overview of recent developments, regarding such optimal navigation problems, from the micro- to the macroscale, and give a perspective by discussing some of the challenges which are ahead of us. Besides exemplifying an elementary approach to optimal navigation problems, the article focuses on works utilizing machine learning-based methods. Such learning-based approaches can uncover highly efficient navigation strategies even for problems that involve e.g. chaotic, high-dimensional, or unknown environments and are hardly solvable based on conventional analytical or simulation methods.

Reinforcement learning of optimal active particle navigation

The development of self-propelled particles at the micro- and the nanoscale has sparked a huge potential for future applications in active matter physics, microsurgery, and targeted drug delivery. However, while the latter applications provoke the quest on how to optimally navigate towards a target, such as e.g. a cancer cell, there is still no simple way known to determine the optimal route in sufficiently complex environments. Here we develop a machine learning-based approach that allows us, for the first time, to determine the asymptotically optimal path of a self-propelled agent which can freely steer in complex environments. Our method hinges on policy gradient-based deep reinforcement learning techniques and, crucially, does not require any reward shaping or heuristics. The presented method provides a powerful alternative to current analytical methods to calculate optimal trajectories and opens a route towards a universal path planner for future intelligent active particles.

Time series model selection with a meta-learning approach; evidence from a pool of forecasting algorithms

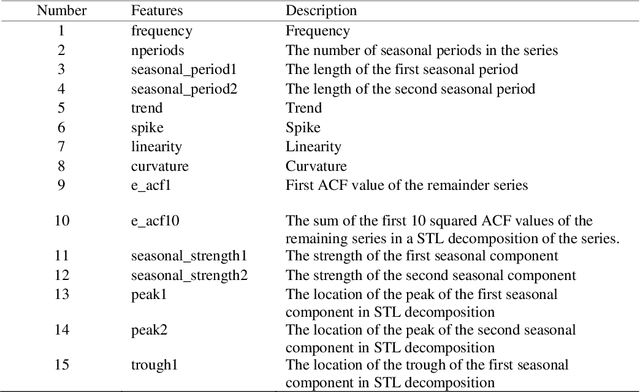
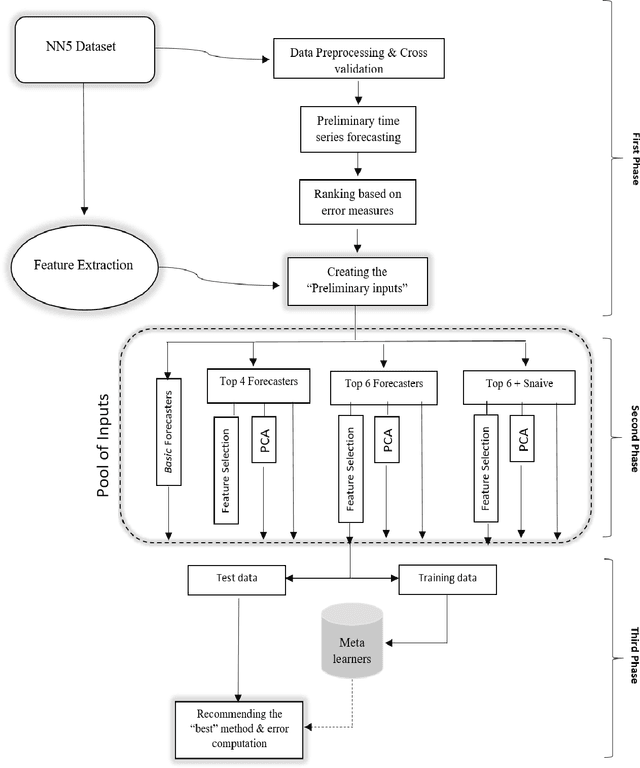
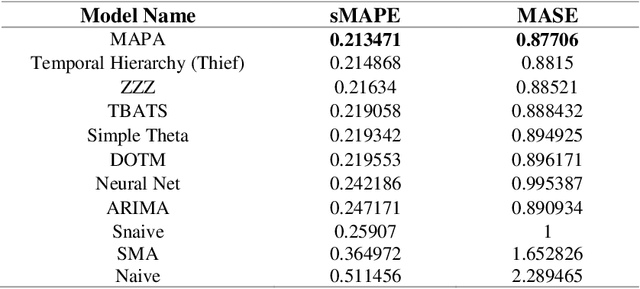
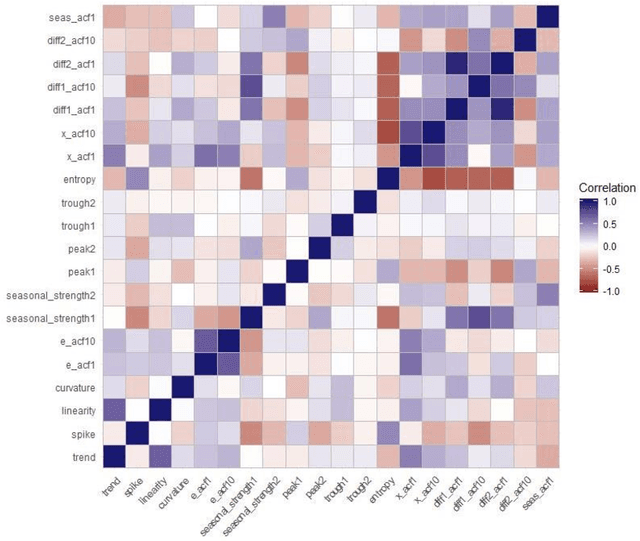
One of the challenging questions in time series forecasting is how to find the best algorithm. In recent years, a recommender system scheme has been developed for time series analysis using a meta-learning approach. This system selects the best forecasting method with consideration of the time series characteristics. In this paper, we propose a novel approach to focusing on some of the unanswered questions resulting from the use of meta-learning in time series forecasting. Therefore, three main gaps in previous works are addressed including, analyzing various subsets of top forecasters as inputs for meta-learners; evaluating the effect of forecasting error measures; and assessing the role of the dimensionality of the feature space on the forecasting errors of meta-learners. All of these objectives are achieved with the help of a diverse state-of-the-art pool of forecasters and meta-learners. For this purpose, first, a pool of forecasting algorithms is implemented on the NN5 competition dataset and ranked based on the two error measures. Then, six machine-learning classifiers known as meta-learners, are trained on the extracted features of the time series in order to assign the most suitable forecasting method for the various subsets of the pool of forecasters. Furthermore, two-dimensionality reduction methods are implemented in order to investigate the role of feature space dimension on the performance of meta-learners. In general, it was found that meta-learners were able to defeat all of the individual benchmark forecasters; this performance was improved even after applying the feature selection method.