Ma Lei
A Bayesian Approach Toward Robust Multidimensional Ellipsoid-Specific Fitting
Jul 27, 2024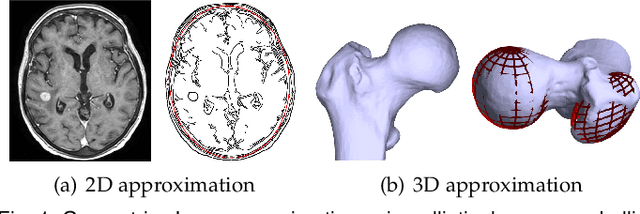

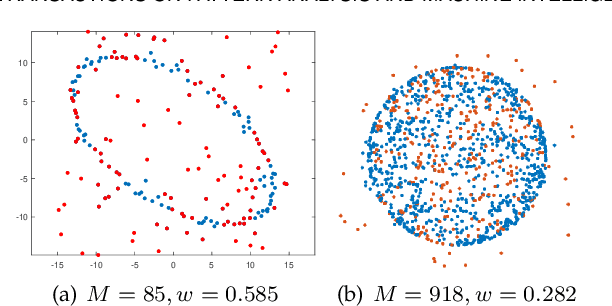
Abstract:This work presents a novel and effective method for fitting multidimensional ellipsoids to scattered data in the contamination of noise and outliers. We approach the problem as a Bayesian parameter estimate process and maximize the posterior probability of a certain ellipsoidal solution given the data. We establish a more robust correlation between these points based on the predictive distribution within the Bayesian framework. We incorporate a uniform prior distribution to constrain the search for primitive parameters within an ellipsoidal domain, ensuring ellipsoid-specific results regardless of inputs. We then establish the connection between measurement point and model data via Bayes' rule to enhance the method's robustness against noise. Due to independent of spatial dimensions, the proposed method not only delivers high-quality fittings to challenging elongated ellipsoids but also generalizes well to multidimensional spaces. To address outlier disturbances, often overlooked by previous approaches, we further introduce a uniform distribution on top of the predictive distribution to significantly enhance the algorithm's robustness against outliers. We introduce an {\epsilon}-accelerated technique to expedite the convergence of EM considerably. To the best of our knowledge, this is the first comprehensive method capable of performing multidimensional ellipsoid specific fitting within the Bayesian optimization paradigm under diverse disturbances. We evaluate it across lower and higher dimensional spaces in the presence of heavy noise, outliers, and substantial variations in axis ratios. Also, we apply it to a wide range of practical applications such as microscopy cell counting, 3D reconstruction, geometric shape approximation, and magnetometer calibration tasks.
GraphReg: Dynamical Point Cloud Registration with Geometry-aware Graph Signal Processing
Feb 02, 2023

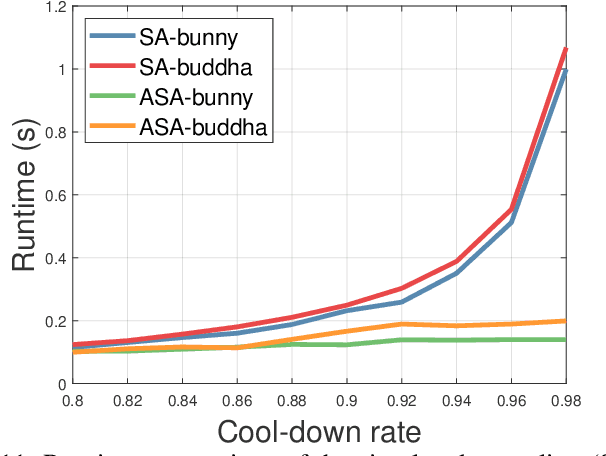
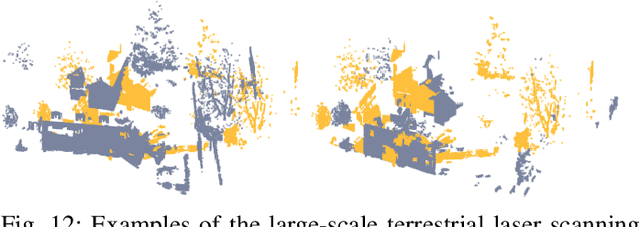
Abstract:This study presents a high-accuracy, efficient, and physically induced method for 3D point cloud registration, which is the core of many important 3D vision problems. In contrast to existing physics-based methods that merely consider spatial point information and ignore surface geometry, we explore geometry aware rigid-body dynamics to regulate the particle (point) motion, which results in more precise and robust registration. Our proposed method consists of four major modules. First, we leverage the graph signal processing (GSP) framework to define a new signature, (i.e., point response intensity for each point), by which we succeed in describing the local surface variation, resampling keypoints, and distinguishing different particles. Then, to address the shortcomings of current physics-based approaches that are sensitive to outliers, we accommodate the defined point response intensity to median absolute deviation (MAD) in robust statistics and adopt the X84 principle for adaptive outlier depression, ensuring a robust and stable registration. Subsequently, we propose a novel geometric invariant under rigid transformations to incorporate higher-order features of point clouds, which is further embedded for force modeling to guide the correspondence between pairwise scans credibly. Finally, we introduce an adaptive simulated annealing (ASA) method to search for the global optimum and substantially accelerate the registration process. We perform comprehensive experiments to evaluate the proposed method on various datasets captured from range scanners to LiDAR. Results demonstrate that our proposed method outperforms representative state-of-the-art approaches in terms of accuracy and is more suitable for registering large-scale point clouds. Furthermore, it is considerably faster and more robust than most competitors.
Robust Ellipsoid-specific Fitting via Expectation Maximization
Oct 26, 2021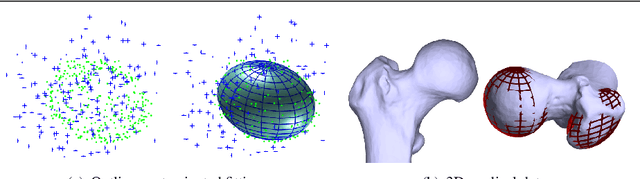
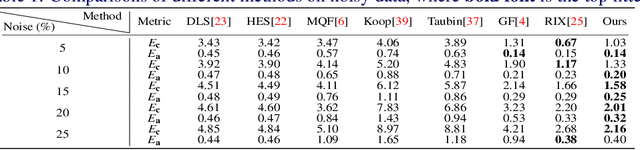

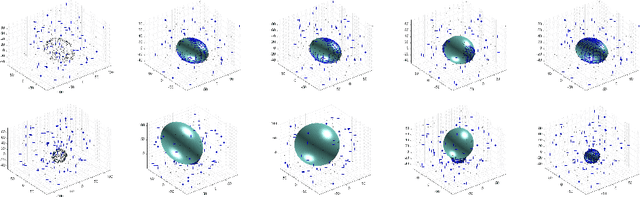
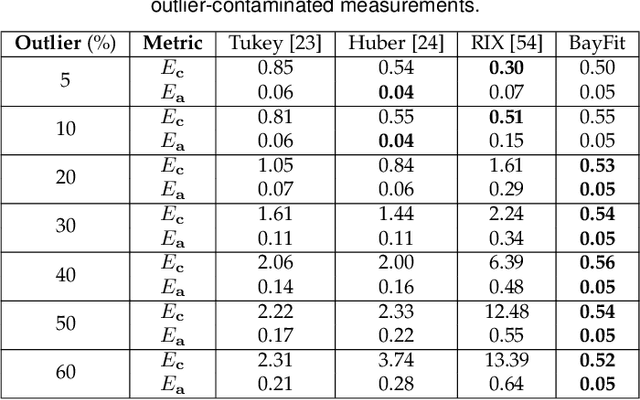
Abstract:Ellipsoid fitting is of general interest in machine vision, such as object detection and shape approximation. Most existing approaches rely on the least-squares fitting of quadrics, minimizing the algebraic or geometric distances, with additional constraints to enforce the quadric as an ellipsoid. However, they are susceptible to outliers and non-ellipsoid or biased results when the axis ratio exceeds certain thresholds. To address these problems, we propose a novel and robust method for ellipsoid fitting in a noisy, outlier-contaminated 3D environment. We explicitly model the ellipsoid by kernel density estimation (KDE) of the input data. The ellipsoid fitting is cast as a maximum likelihood estimation (MLE) problem without extra constraints, where a weighting term is added to depress outliers, and then effectively solved via the Expectation-Maximization (EM) framework. Furthermore, we introduce the vector {\epsilon} technique to accelerate the convergence of the original EM. The proposed method is compared with representative state-of-the-art approaches by extensive experiments, and results show that our method is ellipsoid-specific, parameter free, and more robust against noise, outliers, and the large axis ratio. Our implementation is available at https://zikai1.github.io/.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge