On the Capacity of Quantum Private Information Retrieval from MDS-Coded and Colluding Servers

In quantum private information retrieval (QPIR), a user retrieves a classical file from multiple servers by downloading quantum systems without revealing the identity of the file. The QPIR capacity is the maximal achievable ratio of the retrieved file size to the total download size. In this paper, the capacity of QPIR from MDS-coded and colluding servers is studied. Two classes of QPIR, called stabilizer QPIR and dimension squared QPIR induced from classical strongly linear PIR are defined, and the related QPIR capacities are derived. For the non-colluding case, the general QPIR capacity is derived when the number of files goes to infinity. The capacities of symmetric and non-symmetric QPIR with coded and colluding servers are proved to coincide, being double to their classical counterparts. A general statement on the converse bound for QPIR with coded and colluding servers is derived showing that the capacities of stabilizer QPIR and dimension squared QPIR induced from any class of PIR are upper bounded by twice the classical capacity of the respective PIR class. The proposed capacity-achieving scheme combines the star-product scheme by Freij-Hollanti et al. and the stabilizer QPIR scheme by Song et al. by employing (weakly) self-dual Reed--Solomon codes.

High-Rate Quantum Private Information Retrieval with Weakly Self-Dual Star Product Codes

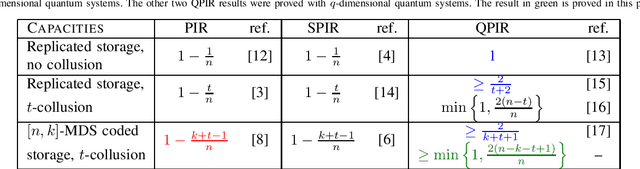
In the classical private information retrieval (PIR) setup, a user wants to retrieve a file from a database or a distributed storage system (DSS) without revealing the file identity to the servers holding the data. In the quantum PIR (QPIR) setting, a user privately retrieves a classical file by receiving quantum information from the servers. The QPIR problem has been treated by Song et al. in the case of replicated servers, both with and without collusion. QPIR over $[n,k]$ maximum distance separable (MDS) coded servers was recently considered by Allaix et al., but the collusion was essentially restricted to $t=n-k$ servers. In this paper, the QPIR setting is extended to account for more flexible collusion of servers satisfying $t < n-k+1$. Similarly to the previous cases, the rates achieved are better than those known or conjectured in the classical counterparts, as well as those of the previously proposed coded and colluding QPIR schemes. This is enabled by considering the stabilizer formalism and weakly self-dual generalized Reed--Solomon (GRS) star product codes.