Unassisted Quantitative Evaluation Of Despeckling Filters

SAR (Synthetic Aperture Radar) imaging plays a central role in Remote Sensing due to, among other important features, its ability to provide high-resolution, day-and-night and almost weather-independent images. SAR images are affected from a granular contamination, speckle, that can be described by a multiplicative model. Many despeckling techniques have been proposed in the literature, as well as measures of the quality of the results they provide. Assuming the multiplicative model, the observed image $Z$ is the product of two independent fields: the backscatter $X$ and the speckle $Y$. The result of any speckle filter is $\widehat X$, an estimator of the backscatter $X$, based solely on the observed data $Z$. An ideal estimator would be the one for which the ratio of the observed image to the filtered one $I=Z/\widehat X$ is only speckle: a collection of independent identically distributed samples from Gamma variates. We, then, assess the quality of a filter by the closeness of $I$ to the hypothesis that it is adherent to the statistical properties of pure speckle. We analyze filters through the ratio image they produce with regards to first- and second-order statistics: the former check marginal properties, while the latter verifies lack of structure. A new quantitative image-quality index is then defined, and applied to state-of-the-art despeckling filters. This new measure provides consistent results with commonly used quality measures (equivalent number of looks, PSNR, MSSIM, $\beta$ edge correlation, and preservation of the mean), and ranks the filters results also in agreement with their visual analysis. We conclude our study showing that the proposed measure can be successfully used to optimize the (often many) parameters that define a speckle filter.

Classification of Complex Wishart Matrices with a Diffusion-Reaction System guided by Stochastic Distances

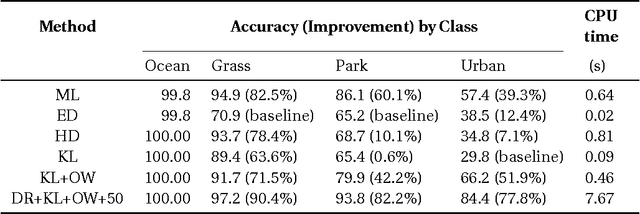
We propose a new method for PolSAR (Polarimetric Synthetic Aperture Radar) imagery classification based on stochastic distances in the space of random matrices obeying complex Wishart distributions. Given a collection of prototypes $\{Z_m\}_{m=1}^M$ and a stochastic distance $d(.,.)$, we classify any random matrix $X$ using two criteria in an iterative setup. Firstly, we associate $X$ to the class which minimizes the weighted stochastic distance $w_md(X,Z_m)$, where the positive weights $w_m$ are computed to maximize the class discrimination power. Secondly, we improve the result by embedding the classification problem into a diffusion-reaction partial differential system where the diffusion term smooths the patches within the image, and the reaction term tends to move the pixel values towards the closest class prototype. In particular, the method inherits the benefits of speckle reduction by diffusion-like methods. Results on synthetic and real PolSAR data show the performance of the method.