Lilyana Mihalkova
Probabilistic Similarity Logic
Mar 15, 2012


Abstract:Many machine learning applications require the ability to learn from and reason about noisy multi-relational data. To address this, several effective representations have been developed that provide both a language for expressing the structural regularities of a domain, and principled support for probabilistic inference. In addition to these two aspects, however, many applications also involve a third aspect-the need to reason about similarities-which has not been directly supported in existing frameworks. This paper introduces probabilistic similarity logic (PSL), a general-purpose framework for joint reasoning about similarity in relational domains that incorporates probabilistic reasoning about similarities and relational structure in a principled way. PSL can integrate any existing domain-specific similarity measures and also supports reasoning about similarities between sets of entities. We provide efficient inference and learning techniques for PSL and demonstrate its effectiveness both in common relational tasks and in settings that require reasoning about similarity.
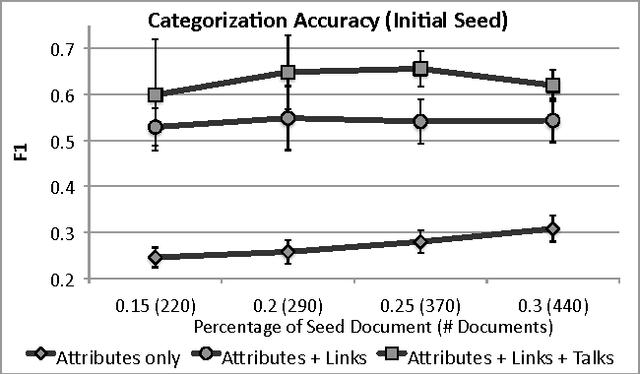
Structure Selection from Streaming Relational Data
Aug 29, 2011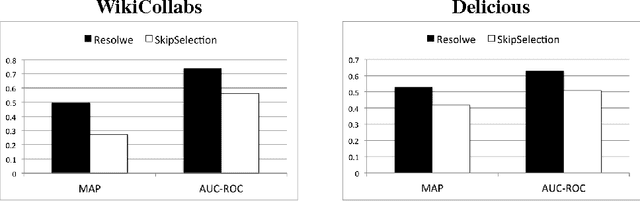

Abstract:Statistical relational learning techniques have been successfully applied in a wide range of relational domains. In most of these applications, the human designers capitalized on their background knowledge by following a trial-and-error trajectory, where relational features are manually defined by a human engineer, parameters are learned for those features on the training data, the resulting model is validated, and the cycle repeats as the engineer adjusts the set of features. This paper seeks to streamline application development in large relational domains by introducing a light-weight approach that efficiently evaluates relational features on pieces of the relational graph that are streamed to it one at a time. We evaluate our approach on two social media tasks and demonstrate that it leads to more accurate models that are learned faster.
Lifted Graphical Models: A Survey
Aug 26, 2011



Abstract:This article presents a survey of work on lifted graphical models. We review a general form for a lifted graphical model, a par-factor graph, and show how a number of existing statistical relational representations map to this formalism. We discuss inference algorithms, including lifted inference algorithms, that efficiently compute the answers to probabilistic queries. We also review work in learning lifted graphical models from data. It is our belief that the need for statistical relational models (whether it goes by that name or another) will grow in the coming decades, as we are inundated with data which is a mix of structured and unstructured, with entities and relations extracted in a noisy manner from text, and with the need to reason effectively with this data. We hope that this synthesis of ideas from many different research groups will provide an accessible starting point for new researchers in this expanding field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge