Evidence Combination and Reasoning and Its Application to Real-World Problem-Solving

In this paper a new mathematical procedure is presented for combining different pieces of evidence which are represented in the interval form to reflect our knowledge about the truth of a hypothesis. Evidences may be correlated to each other (dependent evidences) or conflicting in supports (conflicting evidences). First, assuming independent evidences, we propose a methodology to construct combination rules which obey a set of essential properties. The method is based on a geometric model. We compare results obtained from Dempster-Shafer's rule and the proposed combination rules with both conflicting and non-conflicting data and show that the values generated by proposed combining rules are in tune with our intuition in both cases. Secondly, in the case that evidences are known to be dependent, we consider extensions of the rules derived for handling conflicting evidence. The performance of proposed rules are shown by different examples. The results show that the proposed rules reasonably make decision under dependent evidences

A Study of Scaling Issues in Bayesian Belief Networks for Ship Classification

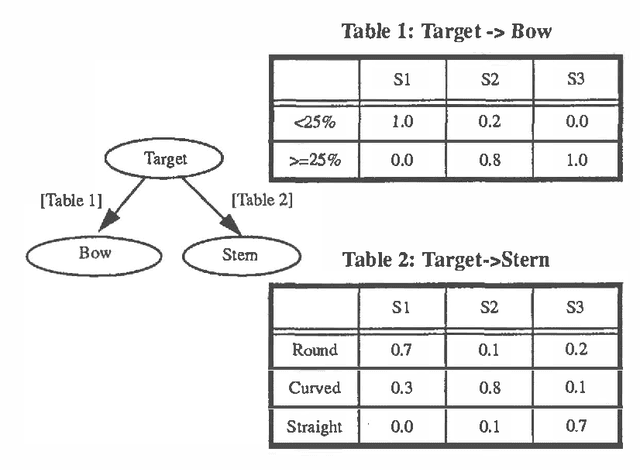
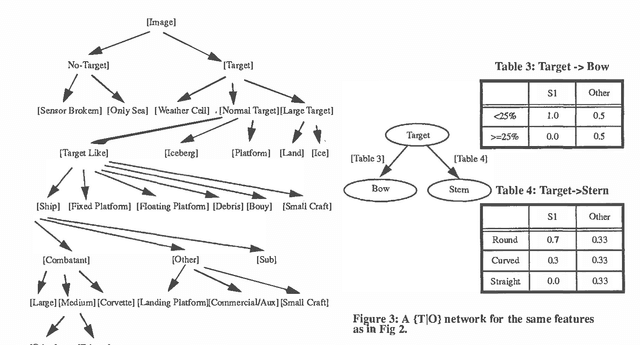
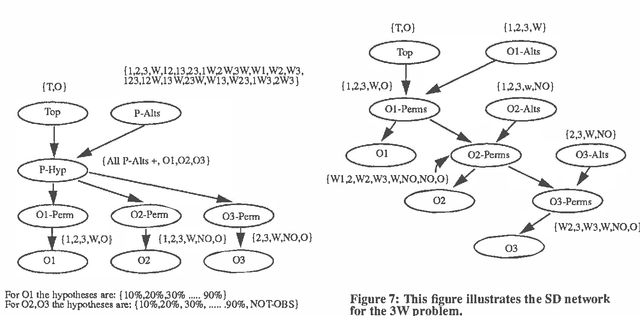
The problems associated with scaling involve active and challenging research topics in the area of artificial intelligence. The purpose is to solve real world problems by means of AI technologies, in cases where the complexity of representation of the real world problem is potentially combinatorial. In this paper, we present a novel approach to cope with the scaling issues in Bayesian belief networks for ship classification. The proposed approach divides the conceptual model of a complex ship classification problem into a set of small modules that work together to solve the classification problem while preserving the functionality of the original model. The possible ways of explaining sensor returns (e.g., the evidence) for some features, such as portholes along the length of a ship, are sometimes combinatorial. Thus, using an exhaustive approach, which entails the enumeration of all possible explanations, is impractical for larger problems. We present a network structure (referred to as Sequential Decomposition, SD) in which each observation is associated with a set of legitimate outcomes which are consistent with the explanation of each observed piece of evidence. The results show that the SD approach allows one to represent feature-observation relations in a manageable way and achieve the same explanatory power as an exhaustive approach.