A Machine Learning Approach to Generate Residual Stress Distributions using Sparse Characterization Data in Friction-Stir Processed Parts

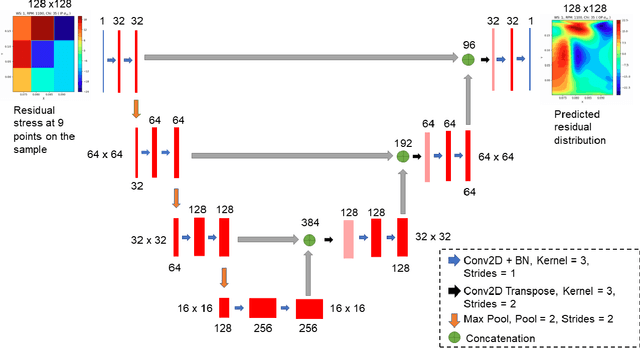
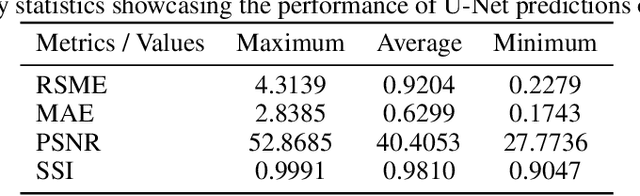
Residual stresses, which remain within a component after processing, can deteriorate performance. Accurately determining their full-field distributions is essential for optimizing the structural integrity and longevity. However, the experimental effort required for full-field characterization is impractical. Given these challenges, this work proposes a machine learning (ML) based Residual Stress Generator (RSG) to infer full-field stresses from limited measurements. An extensive dataset was initially constructed by performing numerous process simulations with a diverse parameter set. A ML model based on U-Net architecture was then trained to learn the underlying structure through systematic hyperparameter tuning. Then, the model's ability to generate simulated stresses was evaluated, and it was ultimately tested on actual characterization data to validate its effectiveness. The model's prediction of simulated stresses shows that it achieved excellent predictive accuracy and exhibited a significant degree of generalization, indicating that it successfully learnt the latent structure of residual stress distribution. The RSG's performance in predicting experimentally characterized data highlights the feasibility of the proposed approach in providing a comprehensive understanding of residual stress distributions from limited measurements, thereby significantly reducing experimental efforts.

Probabilistic Surrogate Model for Accelerating the Design of Electric Vehicle Battery Enclosures for Crash Performance

This paper presents a probabilistic surrogate model for the accelerated design of electric vehicle battery enclosures with a focus on crash performance. The study integrates high-throughput finite element simulations and Gaussian Process Regression to develop a surrogate model that predicts crash parameters with high accuracy while providing uncertainty estimates. The model was trained using data generated from thermoforming and crash simulations over a range of material and process parameters. Validation against new simulation data demonstrated the model's predictive accuracy with mean absolute percentage errors within 8.08% for all output variables. Additionally, a Monte Carlo uncertainty propagation study revealed the impact of input variability on outputs. The results highlight the efficacy of the Gaussian Process Regression model in capturing complex relationships within the dataset, offering a robust and efficient tool for the design optimization of composite battery enclosures.