Kevin B. Schroeder
A Lattice-based Method for Optimization in Continuous Spaces with Genetic Algorithms
Oct 16, 2024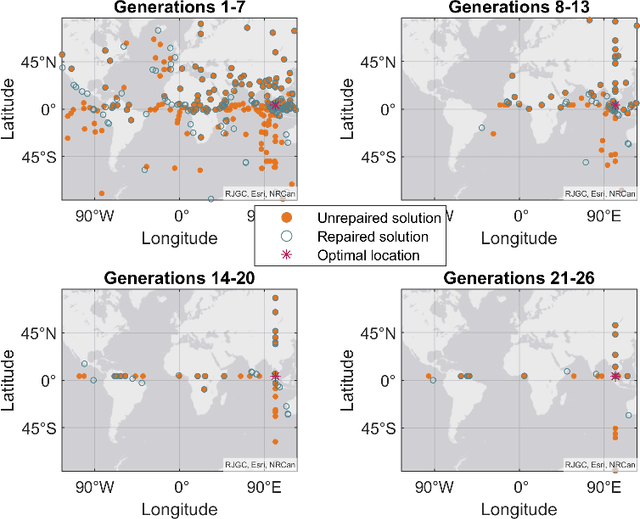

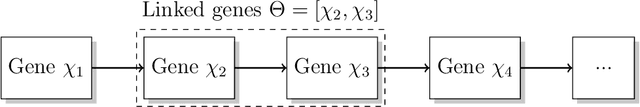
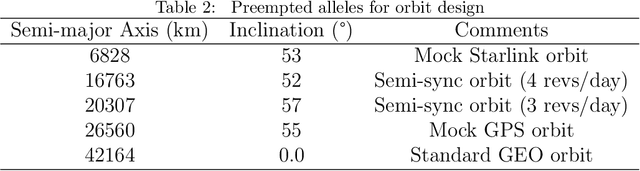
Abstract:This work presents a novel lattice-based methodology for incorporating multidimensional constraints into continuous decision variables within a genetic algorithm (GA) framework. The proposed approach consolidates established transcription techniques for crossover of continuous decision variables, aiming to leverage domain knowledge and guide the search process towards feasible regions of the design space. This work offers a robust and general purpose lattice-based GA that is applicable to a broad range of optimization problems. Monte Carlo analysis demonstrates that lattice-based methods find solutions two orders of magnitude closer to optima in fewer generations. The effectiveness of the lattice-based approach is showcased through two illustrative multi-objective design problems: (1) optimal telescope placement for astrophotography and (2) optimal design of a satellite constellation for maximizing ground station access. The optimal telescope placement example shows that lattice-based methods converge to the Pareto front in 15% fewer generations than traditional methods. The orbit design example shows that lattice-based methods discover an order of magnitude more Pareto-optimal solutions than traditional methods in a highly constrained design space. Overall, the results show that the lattice-based method exhibits enhanced exploration capabilities, traversing the solution space more comprehensively and achieving faster convergence compared to conventional GAs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge