K. V. Srinivas
Thompson Sampling with Virtual Helping Agents
Sep 16, 2022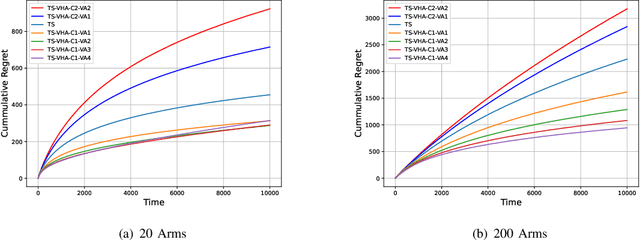
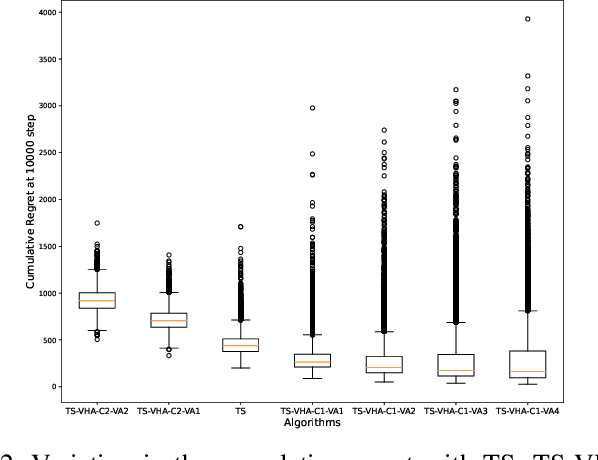
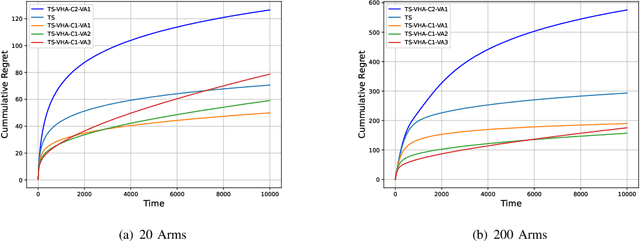
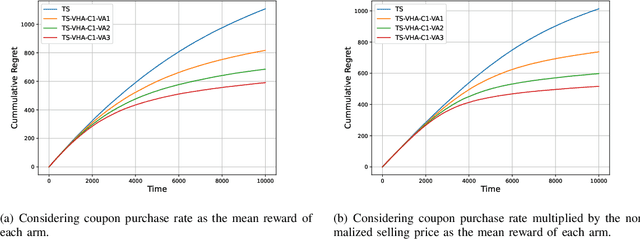
Abstract:We address the problem of online sequential decision making, i.e., balancing the trade-off between exploiting the current knowledge to maximize immediate performance and exploring the new information to gain long-term benefits using the multi-armed bandit framework. Thompson sampling is one of the heuristics for choosing actions that address this exploration-exploitation dilemma. We first propose a general framework that helps heuristically tune the exploration versus exploitation trade-off in Thompson sampling using multiple samples from the posterior distribution. Utilizing this framework, we propose two algorithms for the multi-armed bandit problem and provide theoretical bounds on the cumulative regret. Next, we demonstrate the empirical improvement in the cumulative regret performance of the proposed algorithm over Thompson Sampling. We also show the effectiveness of the proposed algorithm on real-world datasets. Contrary to the existing methods, our framework provides a mechanism to vary the amount of exploration/ exploitation based on the task at hand. Towards this end, we extend our framework for two additional problems, i.e., best arm identification and time-sensitive learning in bandits and compare our algorithm with existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge