Explaining the Success of AdaBoost and Random Forests as Interpolating Classifiers

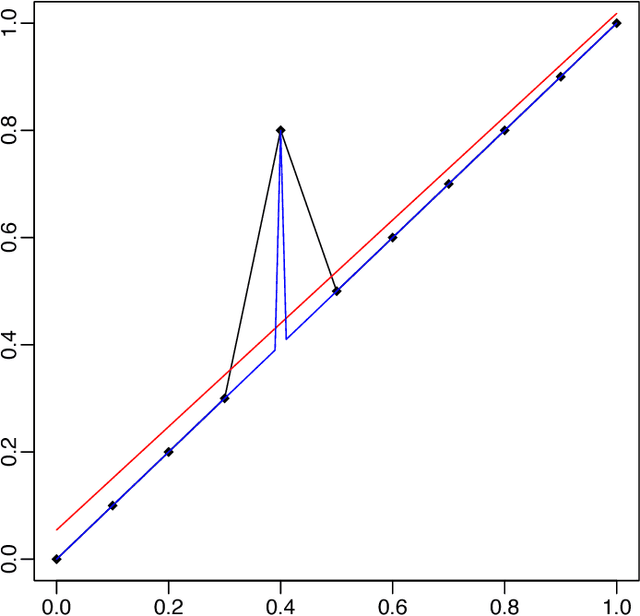
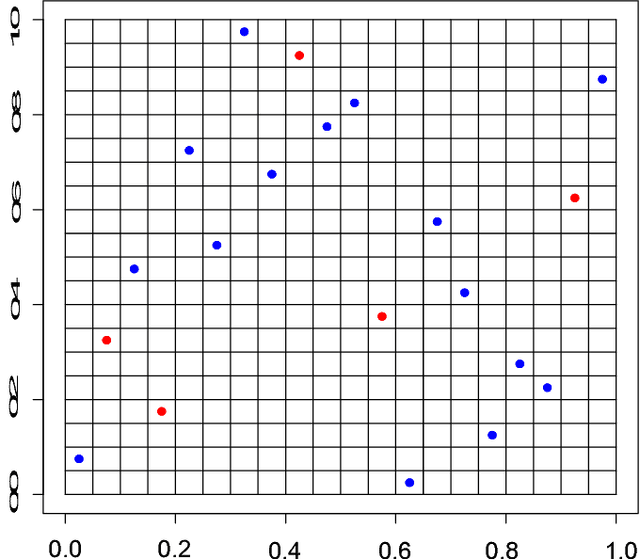
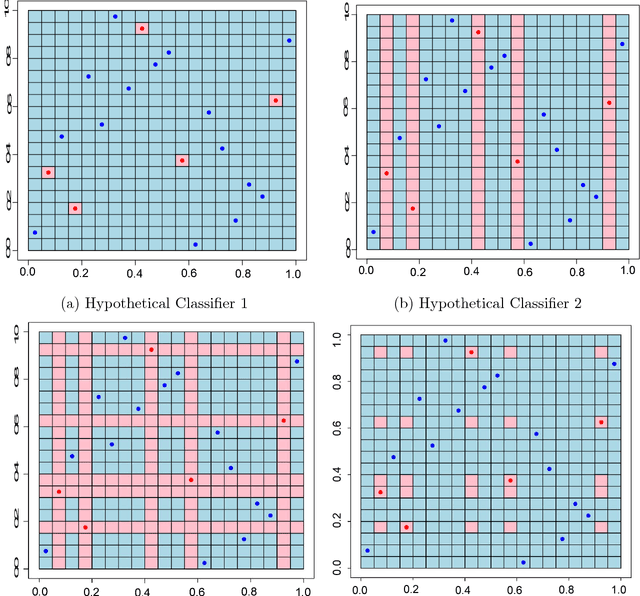
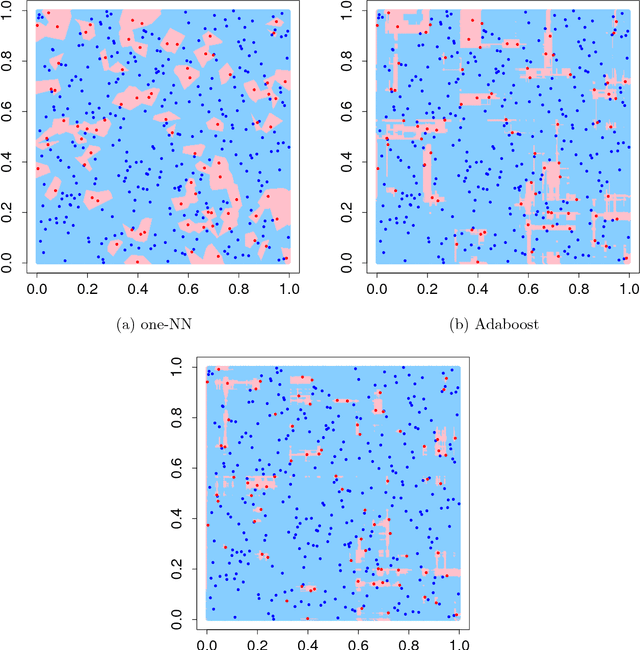
There is a large literature explaining why AdaBoost is a successful classifier. The literature on AdaBoost focuses on classifier margins and boosting's interpretation as the optimization of an exponential likelihood function. These existing explanations, however, have been pointed out to be incomplete. A random forest is another popular ensemble method for which there is substantially less explanation in the literature. We introduce a novel perspective on AdaBoost and random forests that proposes that the two algorithms work for similar reasons. While both classifiers achieve similar predictive accuracy, random forests cannot be conceived as a direct optimization procedure. Rather, random forests is a self-averaging, interpolating algorithm which creates what we denote as a "spikey-smooth" classifier, and we view AdaBoost in the same light. We conjecture that both AdaBoost and random forests succeed because of this mechanism. We provide a number of examples and some theoretical justification to support this explanation. In the process, we question the conventional wisdom that suggests that boosting algorithms for classification require regularization or early stopping and should be limited to low complexity classes of learners, such as decision stumps. We conclude that boosting should be used like random forests: with large decision trees and without direct regularization or early stopping.

bartMachine: Machine Learning with Bayesian Additive Regression Trees

We present a new package in R implementing Bayesian additive regression trees (BART). The package introduces many new features for data analysis using BART such as variable selection, interaction detection, model diagnostic plots, incorporation of missing data and the ability to save trees for future prediction. It is significantly faster than the current R implementation, parallelized, and capable of handling both large sample sizes and high-dimensional data.

Prediction with Missing Data via Bayesian Additive Regression Trees

We present a method for incorporating missing data in non-parametric statistical learning without the need for imputation. We focus on a tree-based method, Bayesian Additive Regression Trees (BART), enhanced with "Missingness Incorporated in Attributes," an approach recently proposed incorporating missingness into decision trees (Twala, 2008). This procedure takes advantage of the partitioning mechanisms found in tree-based models. Simulations on generated models and real data indicate that our proposed method can forecast well on complicated missing-at-random and not-missing-at-random models as well as models where missingness itself influences the response. Our procedure has higher predictive performance and is more stable than competitors in many cases. We also illustrate BART's abilities to incorporate missingness into uncertainty intervals and to detect the influence of missingness on the model fit.