On the Linear Ordering Problem and the Rankability of Data

In 2019, Anderson et al. proposed the concept of rankability, which refers to a dataset's inherent ability to be meaningfully ranked. In this article, we give an expository review of the linear ordering problem (LOP) and then use it to analyze the rankability of data. Specifically, the degree of linearity is used to quantify what percentage of the data aligns with an optimal ranking. In a sports context, this is analogous to the number of games that a ranking can correctly predict in hindsight. In fact, under the appropriate objective function, we show that the optimal rankings computed via the LOP maximize the hindsight accuracy of a ranking. Moreover, we develop a binary program to compute the maximal Kendall tau ranking distance between two optimal rankings, which can be used to measure the diversity among optimal rankings without having to enumerate all optima. Finally, we provide several examples from the world of sports and college rankings to illustrate these concepts and demonstrate our results.

An LP-based Primal Heuristic for 3-Architecture Connected Facility Location in Urban Access Network Design

We investigate the 3-architecture Connected Facility Location Problem arising in the design of urban telecommunication access networks. We propose an original optimization model for the problem that includes additional variables and constraints to take into account wireless signal coverage. Since the problem can prove challenging even for modern state-of-the art optimization solvers, we propose to solve it by an original primal heuristic which combines a probabilistic fixing procedure, guided by peculiar Linear Programming relaxations, with an exact MIP heuristic, based on a very large neighborhood search. Computational experiments on a set of realistic instances show that our heuristic can find solutions associated with much lower optimality gaps than a state-of-the-art solver.

A Fast Hybrid Primal Heuristic for Multiband Robust Capacitated Network Design with Multiple Time Periods

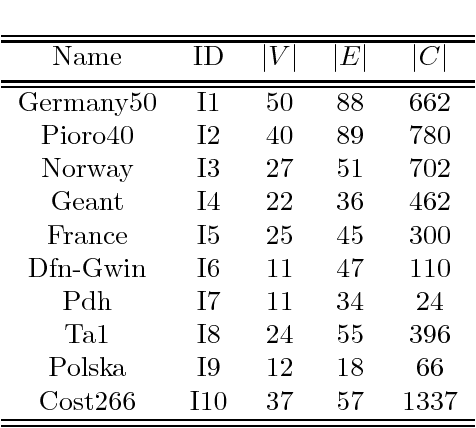
We investigate the Robust Multiperiod Network Design Problem, a generalization of the Capacitated Network Design Problem (CNDP) that, besides establishing flow routing and network capacity installation as in a canonical CNDP, also considers a planning horizon made up of multiple time periods and protection against fluctuations in traffic volumes. As a remedy against traffic volume uncertainty, we propose a Robust Optimization model based on Multiband Robustness (B\"using and D'Andreagiovanni, 2012), a refinement of classical Gamma-Robustness by Bertsimas and Sim that uses a system of multiple deviation bands. Since the resulting optimization problem may prove very challenging even for instances of moderate size solved by a state-of-the-art optimization solver, we propose a hybrid primal heuristic that combines a randomized fixing strategy inspired by ant colony optimization, which exploits information coming from linear relaxations of the problem, and an exact large neighbourhood search. Computational experiments on a set of realistic instances from the SNDlib show that our original heuristic can run fast and produce solutions of extremely high quality associated with low optimality gaps.

A hybrid primal heuristic for Robust Multiperiod Network Design

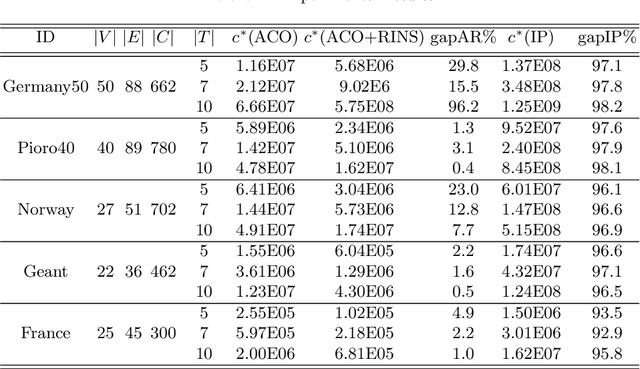
We investigate the Robust Multiperiod Network Design Problem, a generalization of the classical Capacitated Network Design Problem that additionally considers multiple design periods and provides solutions protected against traffic uncertainty. Given the intrinsic difficulty of the problem, which proves challenging even for state-of-the art commercial solvers, we propose a hybrid primal heuristic based on the combination of ant colony optimization and an exact large neighborhood search. Computational experiments on a set of realistic instances from the SNDlib show that our heuristic can find solutions of extremely good quality with low optimality gap.