H-AddiVortes: Heteroscedastic (Bayesian) Additive Voronoi Tessellations

This paper introduces the Heteroscedastic AddiVortes model, a Bayesian non-parametric regression framework that simultaneously models the conditional mean and variance of a response variable using adaptive Voronoi tessellations. By employing a sum-of-tessellations approach for the mean and a product-of-tessellations approach for the variance, the model provides a flexible and interpretable means to capture complex, predictor-dependent relationships and heteroscedastic patterns in data. This dual-layer representation enables precise inference, even in high-dimensional settings, while maintaining computational feasibility through efficient Markov Chain Monte Carlo (MCMC) sampling and conjugate prior structures. We illustrate the model's capability through both simulated and real-world datasets, demonstrating its ability to capture nuanced variance structures, provide reliable predictive uncertainty quantification, and highlight key predictors influencing both the mean response and its variability. Empirical results show that the Heteroscedastic AddiVortes model offers a substantial improvement in capturing distributional properties compared to both homoscedastic and heteroscedastic alternatives, making it a robust tool for complex regression problems in various applied settings.

Eliciting judgements about dependent quantities of interest: The SHELF extension and copula methods illustrated using an asthma case study

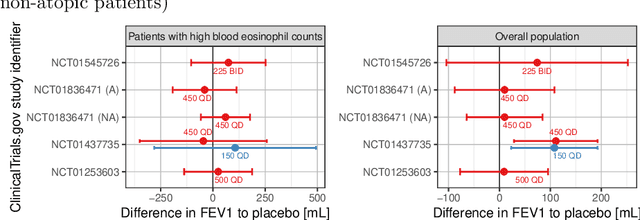
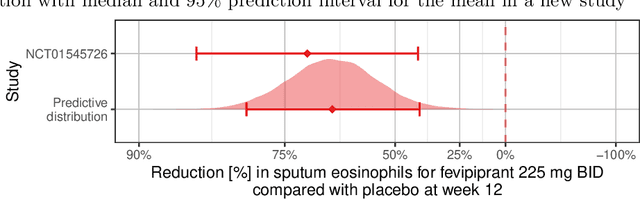
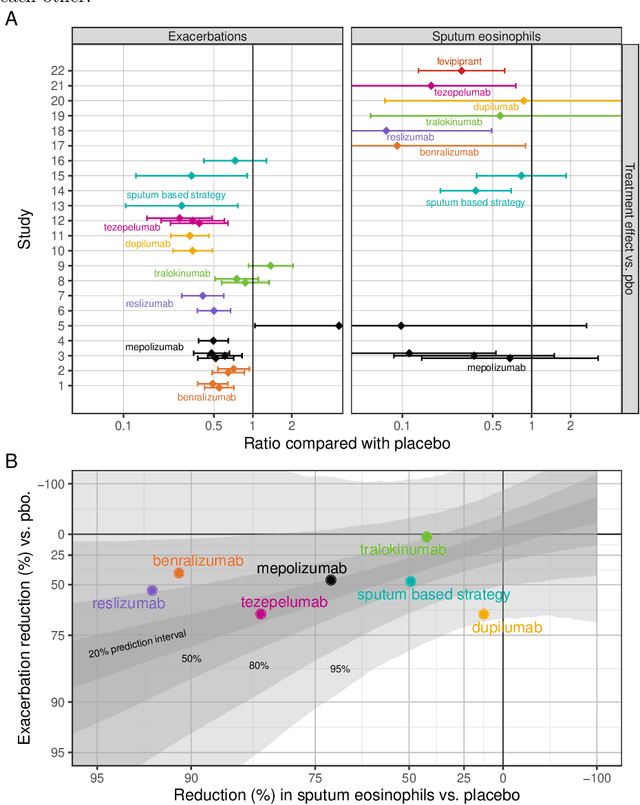
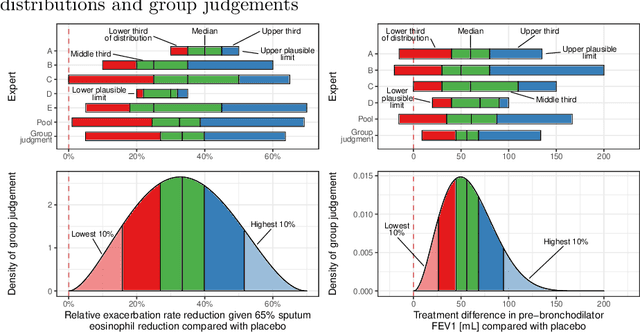
Pharmaceutical companies regularly need to make decisions about drug development programs based on the limited knowledge from early stage clinical trials. In this situation, eliciting the judgements of experts is an attractive approach for synthesising evidence on the unknown quantities of interest. When calculating the probability of success for a drug development program, multiple quantities of interest - such as the effect of a drug on different endpoints - should not be treated as unrelated. We discuss two approaches for establishing a multivariate distribution for several related quantities within the SHeffield ELicitation Framework (SHELF). The first approach elicits experts' judgements about a quantity of interest conditional on knowledge about another one. For the second approach, we first elicit marginal distributions for each quantity of interest. Then, for each pair of quantities, we elicit the concordance probability that both lie on the same side of their respective elicited medians. This allows us to specify a copula to obtain the joint distribution of the quantities of interest. We show how these approaches were used in an elicitation workshop that was performed to assess the probability of success of the registrational program of an asthma drug. The judgements of the experts, which were obtained prior to completion of the pivotal studies, were well aligned with the final trial results.

Rank Pruning for Dominance Queries in CP-Nets

Conditional preference networks (CP-nets) are a graphical representation of a person's (conditional) preferences over a set of discrete variables. In this paper, we introduce a novel method of quantifying preference for any given outcome based on a CP-net representation of a user's preferences. We demonstrate that these values are useful for reasoning about user preferences. In particular, they allow us to order (any subset of) the possible outcomes in accordance with the user's preferences. Further, these values can be used to improve the efficiency of outcome dominance testing. That is, given a pair of outcomes, we can determine which the user prefers more efficiently. Through experimental results, we show that this method is more effective than existing techniques for improving dominance testing efficiency. We show that the above results also hold for CP-nets that express indifference between variable values.

A Bayesian computer model analysis of Robust Bayesian analyses

We harness the power of Bayesian emulation techniques, designed to aid the analysis of complex computer models, to examine the structure of complex Bayesian analyses themselves. These techniques facilitate robust Bayesian analyses and/or sensitivity analyses of complex problems, and hence allow global exploration of the impacts of choices made in both the likelihood and prior specification. We show how previously intractable problems in robustness studies can be overcome using emulation techniques, and how these methods allow other scientists to quickly extract approximations to posterior results corresponding to their own particular subjective specification. The utility and flexibility of our method is demonstrated on a reanalysis of a real application where Bayesian methods were employed to capture beliefs about river flow. We discuss the obvious extensions and directions of future research that such an approach opens up.