John Koo
Popularity Adjusted Block Models are Generalized Random Dot Product Graphs
Sep 09, 2021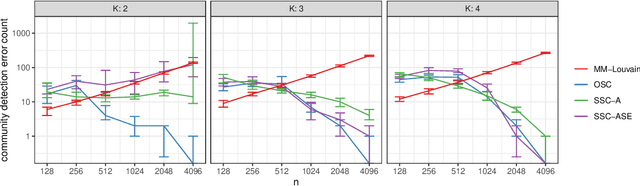
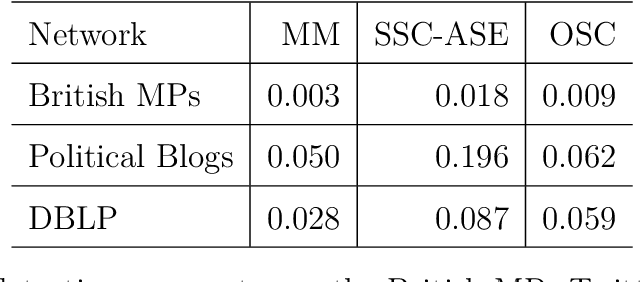
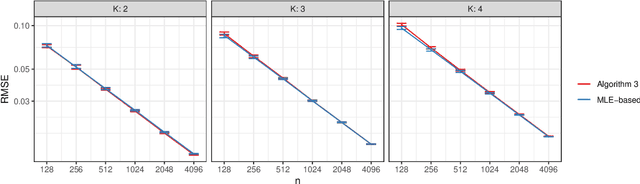

Abstract:We connect two random graph models, the Popularity Adjusted Block Model (PABM) and the Generalized Random Dot Product Graph (GRDPG), by demonstrating that the PABM is a special case of the GRDPG in which communities correspond to mutually orthogonal subspaces of latent vectors. This insight allows us to construct new algorithms for community detection and parameter estimation for the PABM, as well as improve an existing algorithm that relies on Sparse Subspace Clustering. Using established asymptotic properties of Adjacency Spectral Embedding for the GRDPG, we derive asymptotic properties of these algorithms. In particular, we demonstrate that the absolute number of community detection errors tends to zero as the number of graph vertices tends to infinity. Simulation experiments illustrate these properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge