Fractal descriptors based on the probability dimension: a texture analysis and classification approach

In this work, we propose a novel technique for obtaining descriptors of gray-level texture images. The descriptors are provided by applying a multiscale transform to the fractal dimension of the image estimated through the probability (Voss) method. The effectiveness of the descriptors is verified in a classification task using benchmark over texture datasets. The results obtained demonstrate the efficiency of the proposed method as a tool for the description and discrimination of texture images.

Brachiaria species identification using imaging techniques based on fractal descriptors

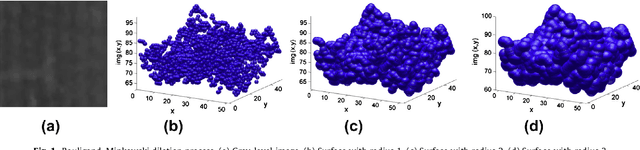
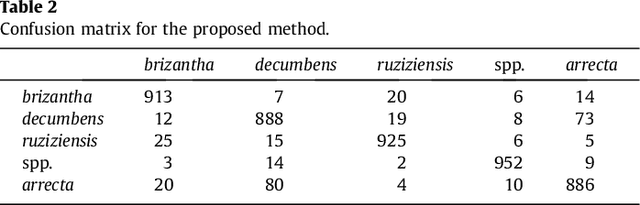
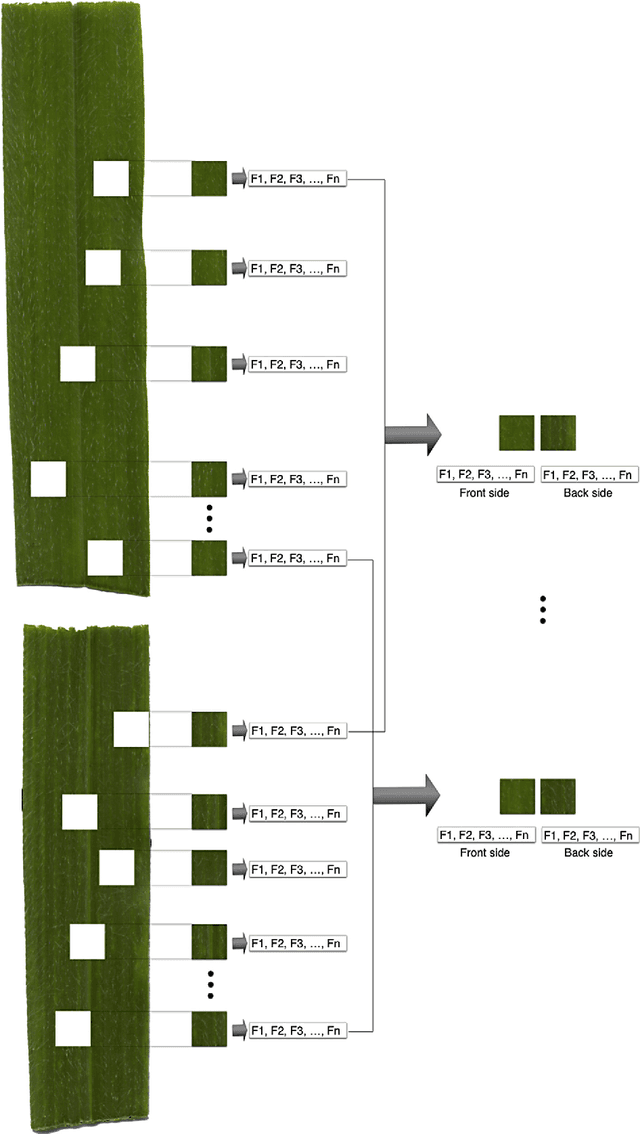
The use of a rapid and accurate method in diagnosis and classification of species and/or cultivars of forage has practical relevance, scientific and trade in various areas of study. Thus, leaf samples of fodder plant species \textit{Brachiaria} were previously identified, collected and scanned to be treated by means of artificial vision to make the database and be used in subsequent classifications. Forage crops used were: \textit{Brachiaria decumbens} cv. IPEAN; \textit{Brachiaria ruziziensis} Germain \& Evrard; \textit{Brachiaria Brizantha} (Hochst. ex. A. Rich.) Stapf; \textit{Brachiaria arrecta} (Hack.) Stent. and \textit{Brachiaria spp}. The images were analyzed by the fractal descriptors method, where a set of measures are obtained from the values of the fractal dimension at different scales. Therefore such values are used as inputs for a state-of-the-art classifier, the Support Vector Machine, which finally discriminates the images according to the respective species.

Multiscale Fractal Descriptors Applied to Texture Classification

This work proposes the combination of multiscale transform with fractal descriptors employed in the classification of gray-level texture images. We apply the space-scale transform (derivative + Gaussian filter) over the Bouligand-Minkowski fractal descriptors, followed by a threshold over the filter response, aiming at attenuating noise effects caused by the final part of this response. The method is tested in the classification of a well-known data set (Brodatz) and compared with other classical texture descriptor techniques. The results demonstrate the advantage of the proposed approach, achieving a higher success rate with a reduced amount of descriptors.

Fractal Descriptors in the Fourier Domain Applied to Color Texture Analysis

The present work proposes the development of a novel method to provide descriptors for colored texture images. The method consists in two steps. In the first, we apply a linear transform in the color space of the image aiming at highlighting spatial structuring relations among the color of pixels. In a second moment, we apply a multiscale approach to the calculus of fractal dimension based on Fourier transform. From this multiscale operation, we extract the descriptors used to discriminate the texture represented in digital images. The accuracy of the method is verified in the classification of two color texture datasets, by comparing the performance of the proposed technique to other classical and state-of-the-art methods for color texture analysis. The results showed an advantage of almost 3% of the proposed technique over the second best approach.

Fractal Descriptors Based on Fourier Spectrum Applied to Texture Analysis

This work proposes the development and study of a novel technique for the generation of fractal descriptors used in texture analysis. The novel descriptors are obtained from a multiscale transform applied to the Fourier technique of fractal dimension calculus. The power spectrum of the Fourier transform of the image is plotted against the frequency in a log- log scale and a multiscale transform is applied to this curve. The obtained values are taken as the fractal descriptors of the image. The validation of the propose is performed by the use of the descriptors for the classification of a dataset of texture images whose real classes are previously known. The classification precision is compared to other fractal descriptors known in the literature. The results confirm the efficiency of the proposed method.

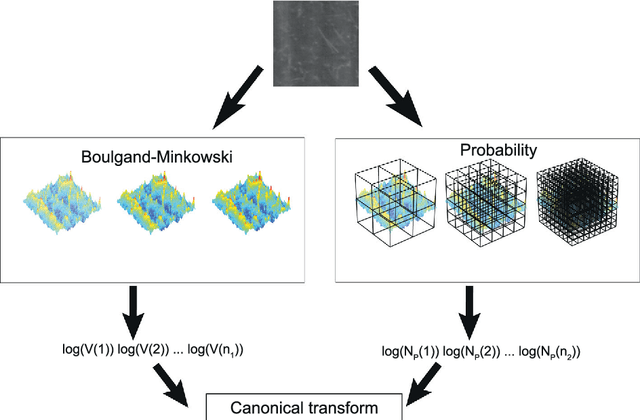
Enhancing Volumetric Bouligand-Minkowski Fractal Descriptors by using Functional Data Analysis

This work proposes and study the concept of Functional Data Analysis transform, applying it to the performance improving of volumetric Bouligand-Minkowski fractal descriptors. The proposed transform consists essentially in changing the descriptors originally defined in the space of the calculus of fractal dimension into the space of coefficients used in the functional data representation of these descriptors. The transformed decriptors are used here in texture classification problems. The enhancement provided by the FDA transform is measured by comparing the transformed to the original descriptors in terms of the correctness rate in the classification of well known datasets.