Implicit Regularization for Group Sparsity

We study the implicit regularization of gradient descent towards structured sparsity via a novel neural reparameterization, which we call a diagonally grouped linear neural network. We show the following intriguing property of our reparameterization: gradient descent over the squared regression loss, without any explicit regularization, biases towards solutions with a group sparsity structure. In contrast to many existing works in understanding implicit regularization, we prove that our training trajectory cannot be simulated by mirror descent. We analyze the gradient dynamics of the corresponding regression problem in the general noise setting and obtain minimax-optimal error rates. Compared to existing bounds for implicit sparse regularization using diagonal linear networks, our analysis with the new reparameterization shows improved sample complexity. In the degenerate case of size-one groups, our approach gives rise to a new algorithm for sparse linear regression. Finally, we demonstrate the efficacy of our approach with several numerical experiments.

Deep Spatio-Temporal Wind Power Forecasting

Wind power forecasting has drawn increasing attention among researchers as the consumption of renewable energy grows. In this paper, we develop a deep learning approach based on encoder-decoder structure. Our model forecasts wind power generated by a wind turbine using its spatial location relative to other turbines and historical wind speed data. In this way, we effectively integrate spatial dependency and temporal trends to make turbine-specific predictions. The advantages of our method over existing work can be summarized as 1) it directly predicts wind power based on historical wind speed, without the need for prediction of wind speed first, and then using a transformation; 2) it can effectively capture long-term dependency 3) our model is more scalable and efficient compared with other deep learning based methods. We demonstrate the efficacy of our model on the benchmark real-world datasets.

Implicit Sparse Regularization: The Impact of Depth and Early Stopping

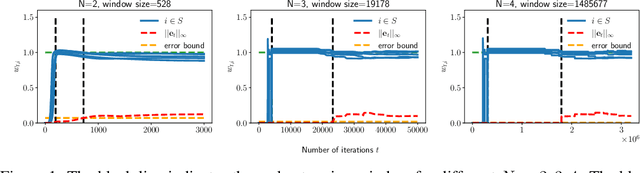
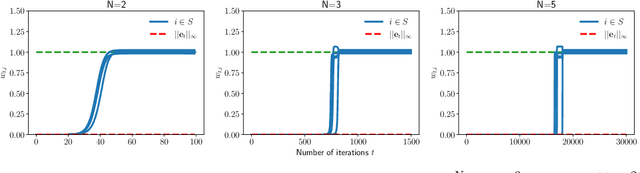
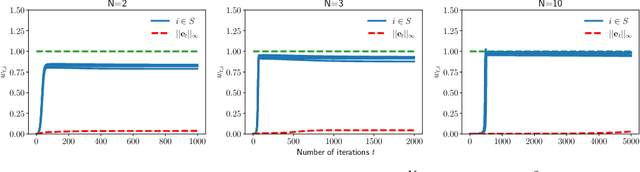
In this paper, we study the implicit bias of gradient descent for sparse regression. We extend results on regression with quadratic parametrization, which amounts to depth-2 diagonal linear networks, to more general depth-N networks, under more realistic settings of noise and correlated designs. We show that early stopping is crucial for gradient descent to converge to a sparse model, a phenomenon that we call implicit sparse regularization. This result is in sharp contrast to known results for noiseless and uncorrelated-design cases. We characterize the impact of depth and early stopping and show that for a general depth parameter N, gradient descent with early stopping achieves minimax optimal sparse recovery with sufficiently small initialization and step size. In particular, we show that increasing depth enlarges the scale of working initialization and the early-stopping window, which leads to more stable gradient paths for sparse recovery.