Discovery of Governing Equations with Recursive Deep Neural Networks

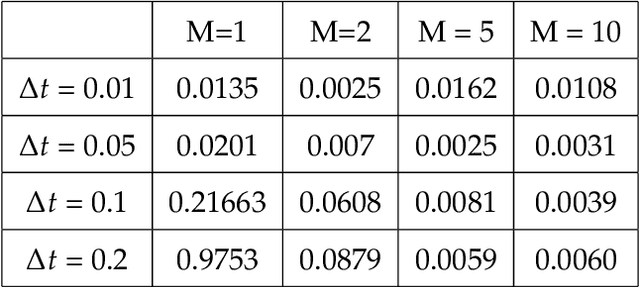
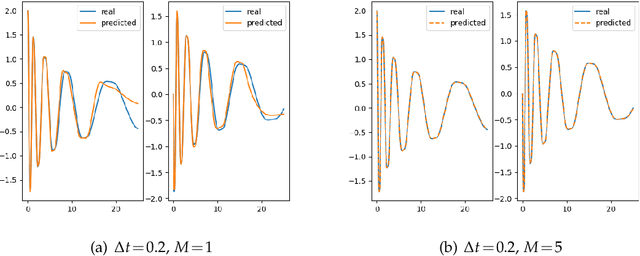
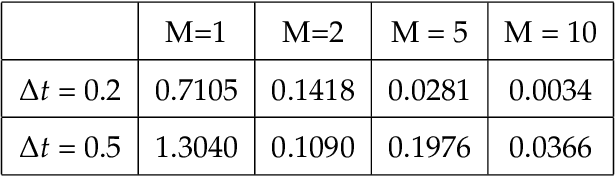
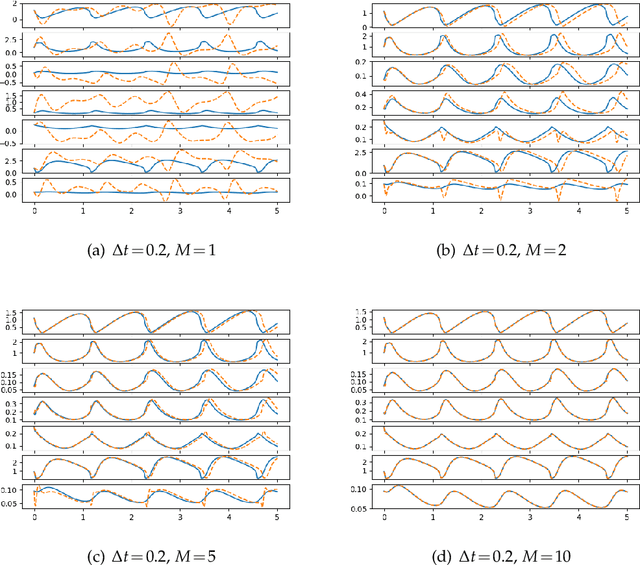
Model discovery based on existing data has been one of the major focuses of mathematical modelers for decades. Despite tremendous achievements of model identification from adequate data, how to unravel the models from limited data is less resolved. In this paper, we focus on the model discovery problem when the data is not efficiently sampled in time. This is common due to limited experimental accessibility and labor/resource constraints. Specifically, we introduce a recursive deep neural network (RDNN) for data-driven model discovery. This recursive approach can retrieve the governing equation in a simple and efficient manner, and it can significantly improve the approximation accuracy by increasing the recursive stages. In particular, our proposed approach shows superior power when the existing data are sampled with a large time lag, from which the traditional approach might not be able to recover the model well. Several widely used examples of dynamical systems are used to benchmark this newly proposed recursive approach. Numerical comparisons confirm the effectiveness of this recursive neural network for model discovery.

Solving Allen-Cahn and Cahn-Hilliard Equations using the Adaptive Physics Informed Neural Networks

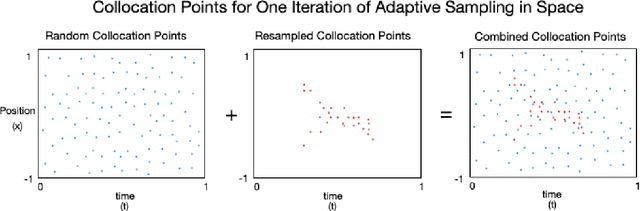
Phase field models, in particular, the Allen-Cahn type and Cahn-Hilliard type equations, have been widely used to investigate interfacial dynamic problems. Designing accurate, efficient, and stable numerical algorithms for solving the phase field models has been an active field for decades. In this paper, we focus on using the deep neural network to design an automatic numerical solver for the Allen-Cahn and Cahn-Hilliard equations by proposing an improved physics informed neural network (PINN). Though the PINN has been embraced to investigate many differential equation problems, we find a direct application of the PINN in solving phase-field equations won't provide accurate solutions in many cases. Thus, we propose various techniques that add to the approximation power of the PINN. As a major contribution of this paper, we propose to embrace the adaptive idea in both space and time and introduce various sampling strategies, such that we are able to improve the efficiency and accuracy of the PINN on solving phase field equations. In addition, the improved PINN has no restriction on the explicit form of the PDEs, making it applicable to a wider class of PDE problems, and shedding light on numerical approximations of other PDEs in general.