3D helical CT reconstruction with memory efficient invertible Learned Primal-Dual method

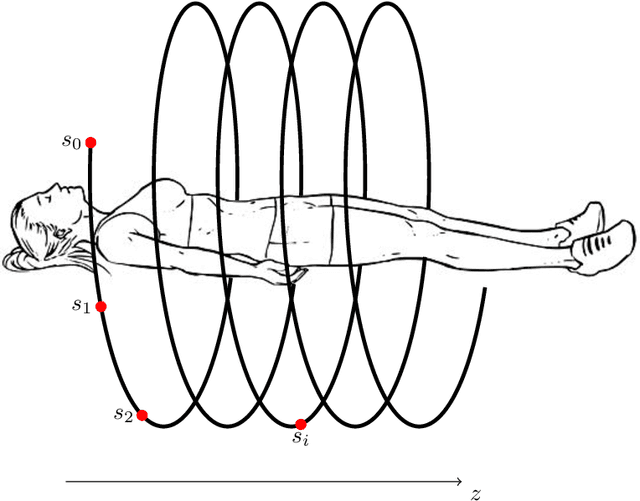
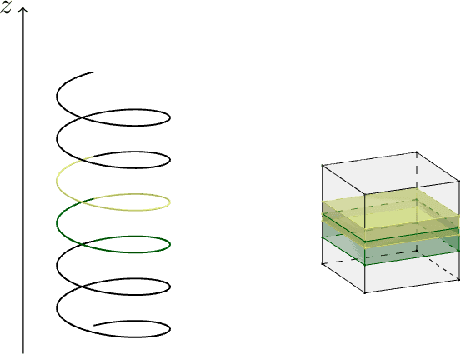
Helical acquisition geometry is the most common geometry used in computed tomography (CT) scanners for medical imaging. We adapt the invertible Learned Primal-Dual (iLPD) deep neural network architecture so that it can be applied to helical 3D CT reconstruction. We achieve this by splitting the geometry and the data in parts that fit the memory and by splitting images into corresponding sub-volumes. The architecture can be applied to images different in size along the rotation axis. We perform the experiments on tomographic data simulated from realistic helical geometries.

Deep learning based dictionary learning and tomographic image reconstruction

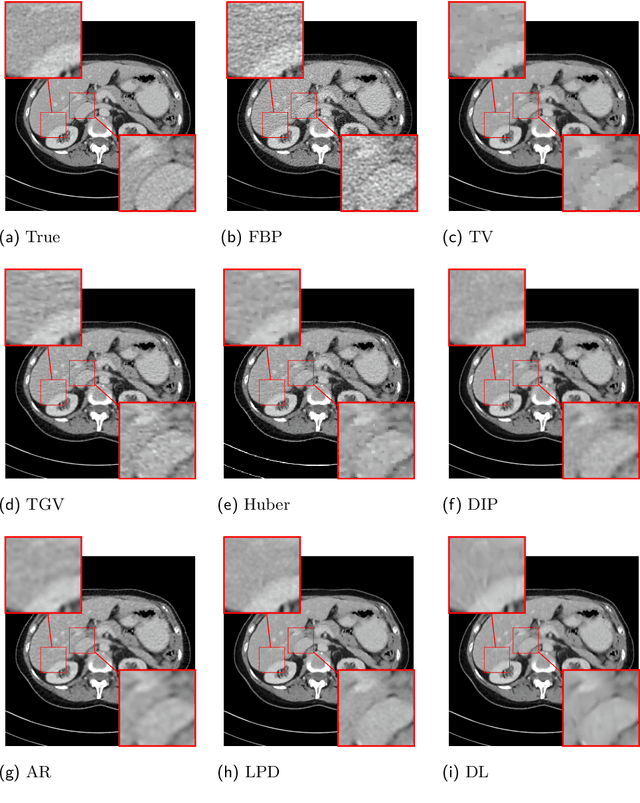
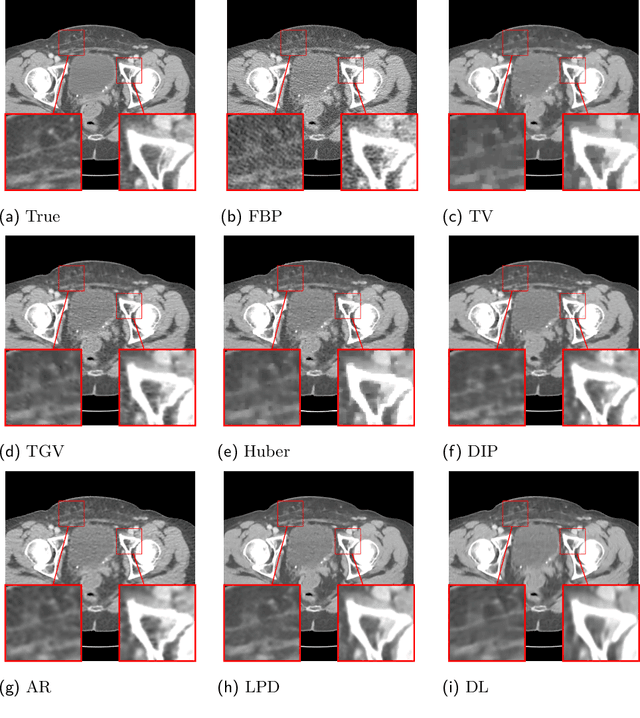
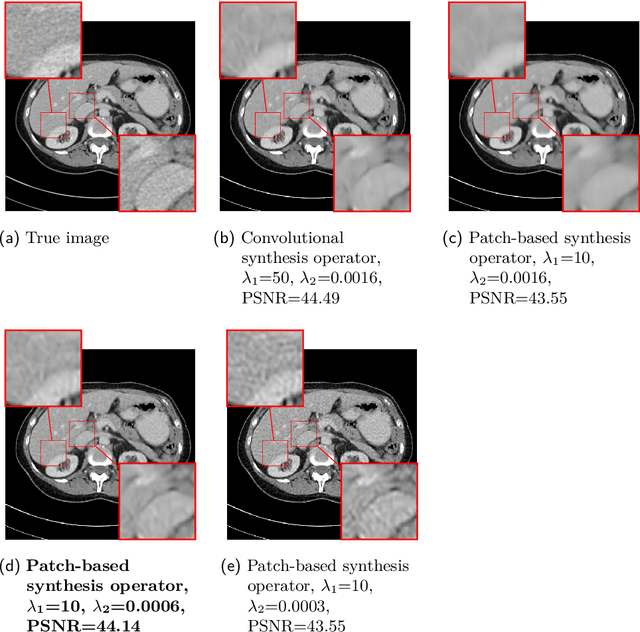
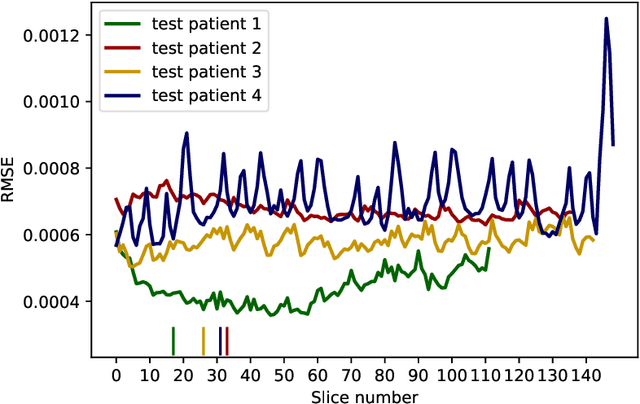
This work presents an approach for image reconstruction in clinical low-dose tomography that combines principles from sparse signal processing with ideas from deep learning. First, we describe sparse signal representation in terms of dictionaries from a statistical perspective and interpret dictionary learning as a process of aligning distribution that arises from a generative model with empirical distribution of true signals. As a result we can see that sparse coding with learned dictionaries resembles a specific variational autoencoder, where the decoder is a linear function and the encoder is a sparse coding algorithm. Next, we show that dictionary learning can also benefit from computational advancements introduced in the context of deep learning, such as parallelism and as stochastic optimization. Finally, we show that regularization by dictionaries achieves competitive performance in computed tomography (CT) reconstruction comparing to state-of-the-art model based and data driven approaches.