Jefferson L. M. A. Gomes
Solving the Discretised Multiphase Flow Equations with Interface Capturing on Structured Grids Using Machine Learning Libraries
Jan 12, 2024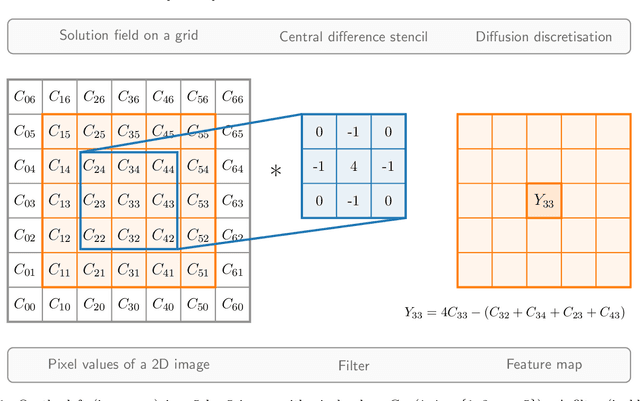
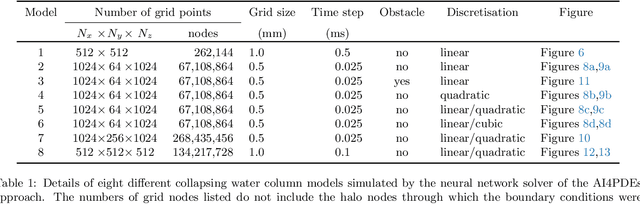
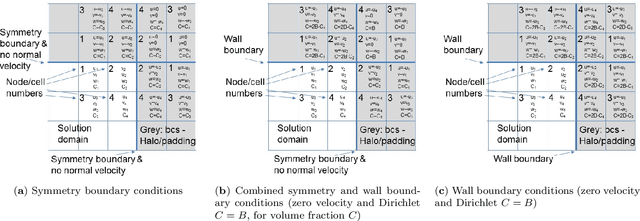

Abstract:This paper solves the multiphase flow equations with interface capturing using the AI4PDEs approach (Artificial Intelligence for Partial Differential Equations). The solver within AI4PDEs uses tools from machine learning (ML) libraries to solve (exactly) partial differential equations (PDEs) that have been discretised using numerical methods. Convolutional layers can be used to express the discretisations as a neural network, whose weights are determined by the numerical method, rather than by training. To solve the system, a multigrid solver is implemented through a neural network with a U-Net architecture. Immiscible two-phase flow is modelled by the 3D incompressible Navier-Stokes equations with surface tension and advection of a volume fraction field, which describes the interface between the fluids. A new compressive algebraic volume-of-fluids method is introduced, based on a residual formulation using Petrov-Galerkin for accuracy and designed with AI4PDEs in mind. High-order finite-element based schemes are chosen to model a collapsing water column and a rising bubble. Results compare well with experimental data and other numerical results from the literature, demonstrating that, for the first time, finite element discretisations of multiphase flows can be solved using the neural network solver from the AI4PDEs approach. A benefit of expressing numerical discretisations as neural networks is that the code can run, without modification, on CPUs, GPUs or the latest accelerators designed especially to run AI codes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge