A Reinforcement Learning Approach for Transient Control of Liquid Rocket Engines

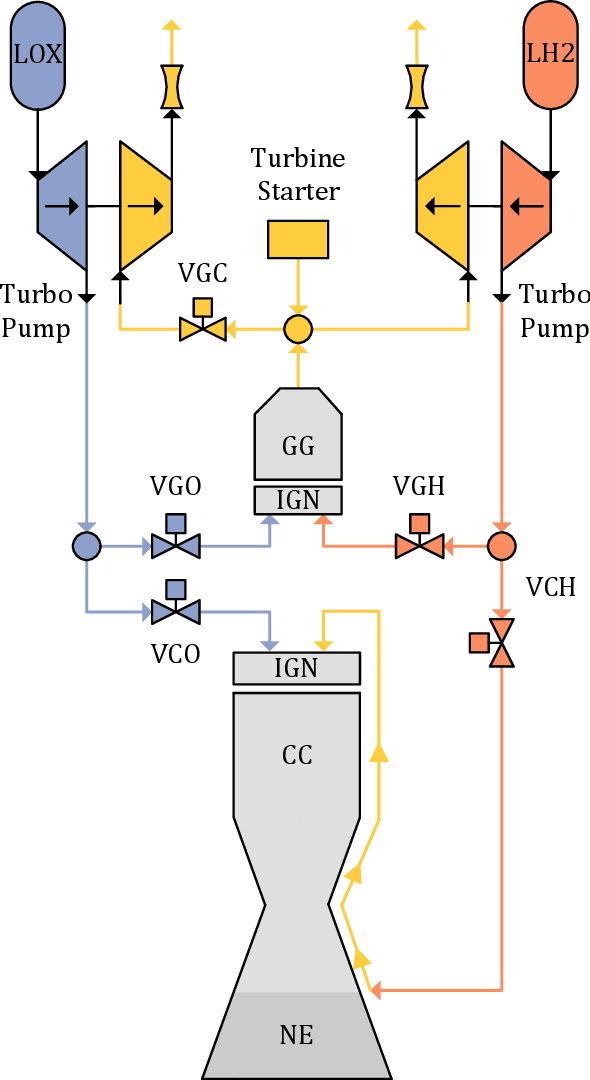
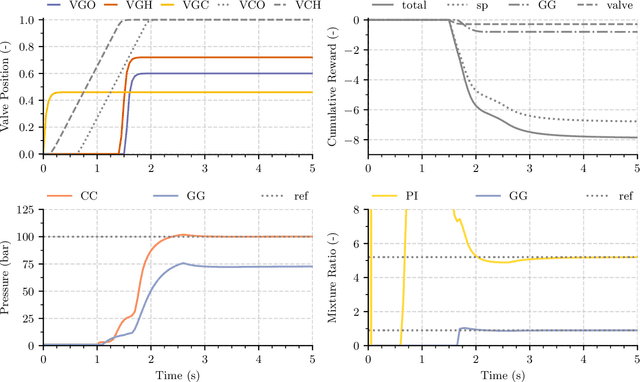
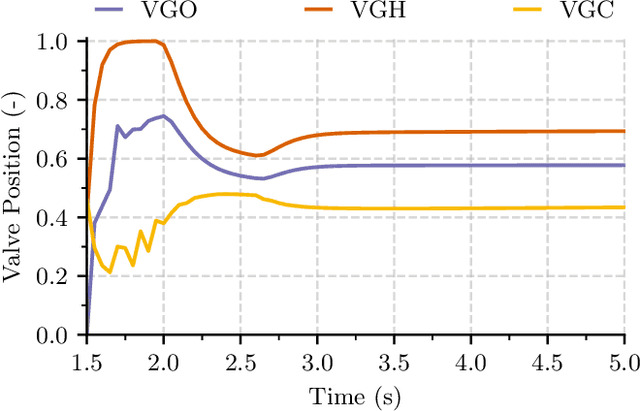
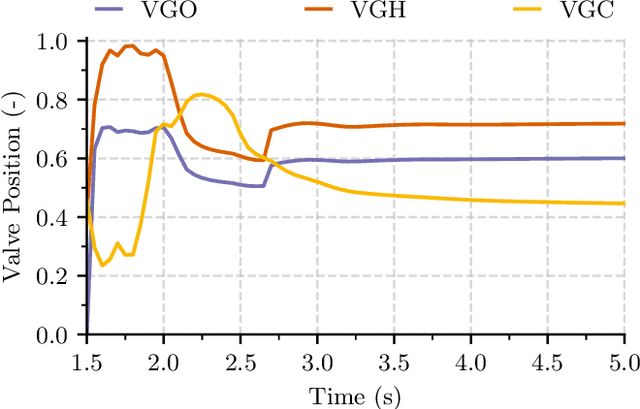
Nowadays, liquid rocket engines use closed-loop control at most near steady operating conditions. The control of the transient phases is traditionally performed in open-loop due to highly nonlinear system dynamics. This situation is unsatisfactory, in particular for reusable engines. The open-loop control system cannot provide optimal engine performance due to external disturbances or the degeneration of engine components over time. In this paper, we study a deep reinforcement learning approach for optimal control of a generic gas-generator engine's continuous start-up phase. It is shown that the learned policy can reach different steady-state operating points and convincingly adapt to changing system parameters. A quantitative comparison with carefully tuned open-loop sequences and PID controllers is included. The deep reinforcement learning controller achieves the highest performance and requires only minimal computational effort to calculate the control action, which is a big advantage over approaches that require online optimization, such as model predictive control. control.

Heat Transfer Prediction for Methane in Regenerative Cooling Channels with Neural Networks

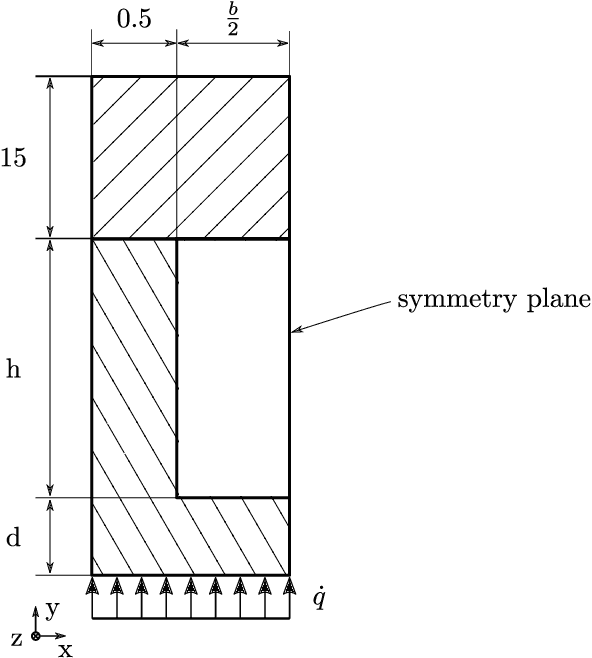
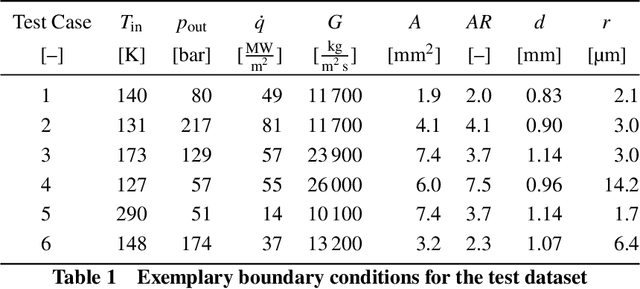
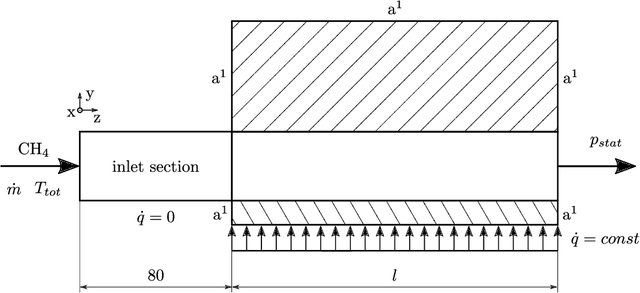
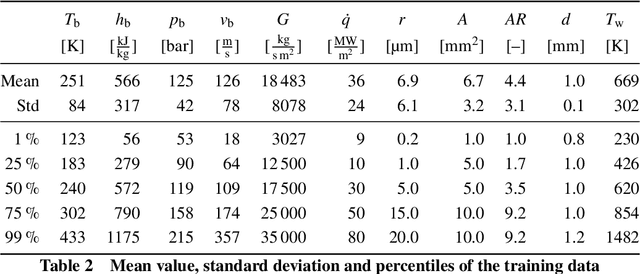
Methane is considered being a good choice as a propellant for future reusable launch systems. However, the heat transfer prediction for supercritical methane flowing in cooling channels of a regeneratively cooled combustion chamber is challenging. Because accurate heat transfer predictions are essential to design reliable and efficient cooling systems, heat transfer modeling is a fundamental issue to address. Advanced computational fluid dynamics (CFD) calculations achieve sufficient accuracy, but the associated computational cost prevents an efficient integration in optimization loops. Surrogate models based on artificial neural networks (ANNs) offer a great speed advantage. It is shown that an ANN, trained on data extracted from samples of CFD simulations, is able to predict the maximum wall temperature along straight rocket engine cooling channels using methane with convincing precision. The combination of the ANN model with simple relations for pressure drop and enthalpy rise results in a complete reduced order model, which can be used for numerically efficient design space exploration and optimization.