Jamal F. Husseini
Probabilistic Neural Networks (PNNs) for Modeling Aleatoric Uncertainty in Scientific Machine Learning
Feb 21, 2024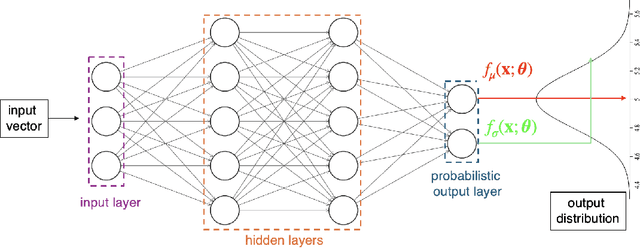
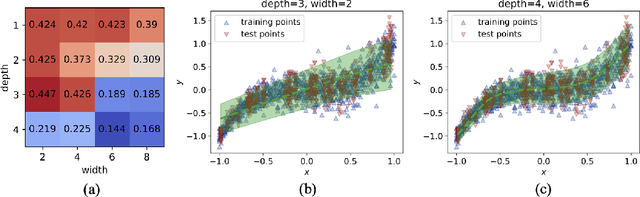
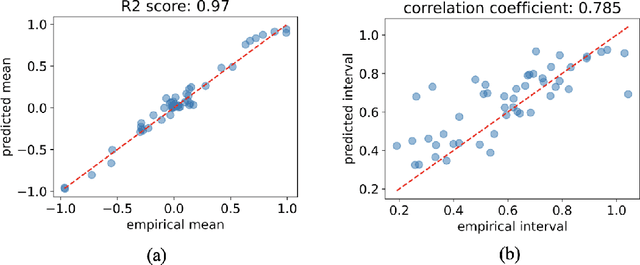
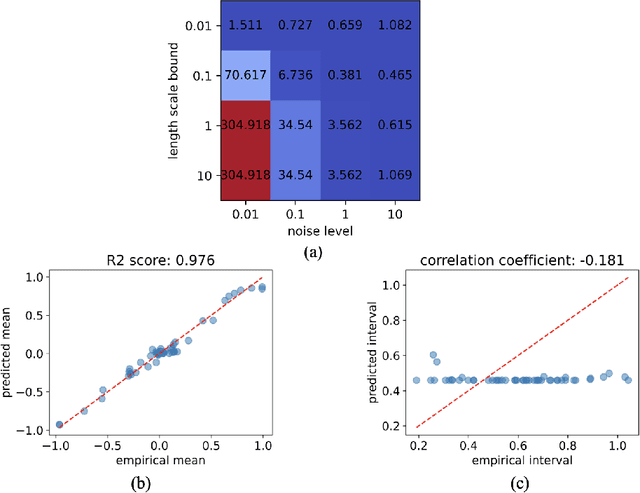
Abstract:This paper investigates the use of probabilistic neural networks (PNNs) to model aleatoric uncertainty, which refers to the inherent variability in the input-output relationships of a system, often characterized by unequal variance or heteroscedasticity. Unlike traditional neural networks that produce deterministic outputs, PNNs generate probability distributions for the target variable, allowing the determination of both predicted means and intervals in regression scenarios. Contributions of this paper include the development of a probabilistic distance metric to optimize PNN architecture, and the deployment of PNNs in controlled data sets as well as a practical material science case involving fiber-reinforced composites. The findings confirm that PNNs effectively model aleatoric uncertainty, proving to be more appropriate than the commonly employed Gaussian process regression for this purpose. Specifically, in a real-world scientific machine learning context, PNNs yield remarkably accurate output mean estimates with R-squared scores approaching 0.97, and their predicted intervals exhibit a high correlation coefficient of nearly 0.80, closely matching observed data intervals. Hence, this research contributes to the ongoing exploration of leveraging the sophisticated representational capacity of neural networks to delineate complex input-output relationships in scientific problems.
Two-Stage Surrogate Modeling for Data-Driven Design Optimization with Application to Composite Microstructure Generation
Jan 04, 2024Abstract:This paper introduces a novel two-stage machine learning-based surrogate modeling framework to address inverse problems in scientific and engineering fields. In the first stage of the proposed framework, a machine learning model termed the "learner" identifies a limited set of candidates within the input design space whose predicted outputs closely align with desired outcomes. Subsequently, in the second stage, a separate surrogate model, functioning as an "evaluator," is employed to assess the reduced candidate space generated in the first stage. This evaluation process eliminates inaccurate and uncertain solutions, guided by a user-defined coverage level. The framework's distinctive contribution is the integration of conformal inference, providing a versatile and efficient approach that can be widely applicable. To demonstrate the effectiveness of the proposed framework compared to conventional single-stage inverse problems, we conduct several benchmark tests and investigate an engineering application focused on the micromechanical modeling of fiber-reinforced composites. The results affirm the superiority of our proposed framework, as it consistently produces more reliable solutions. Therefore, the introduced framework offers a unique perspective on fostering interactions between machine learning-based surrogate models in real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge