Learnability with PAC Semantics for Multi-agent Beliefs

The tension between deduction and induction is perhaps the most fundamental issue in areas such as philosophy, cognition and artificial intelligence. In an influential paper, Valiant recognised that the challenge of learning should be integrated with deduction. In particular, he proposed a semantics to capture the quality possessed by the output of Probably Approximately Correct (PAC) learning algorithms when formulated in a logic. Although weaker than classical entailment, it allows for a powerful model-theoretic framework for answering queries. In this paper, we provide a new technical foundation to demonstrate PAC learning with multi-agent epistemic logics. To circumvent the negative results in the literature on the difficulty of robust learning with the PAC semantics, we consider so-called implicit learning where we are able to incorporate observations to the background theory in service of deciding the entailment of an epistemic query. We prove correctness of the learning procedure and discuss results on the sample complexity, that is how many observations we will need to provably assert that the query is entailed given a user-specified error bound. Finally, we investigate under what circumstances this algorithm can be made efficient. On the last point, given that reasoning in epistemic logics especially in multi-agent epistemic logics is PSPACE-complete, it might seem like there is no hope for this problem. We leverage some recent results on the so-called Representation Theorem explored for single-agent and multi-agent epistemic logics with the only knowing operator to reduce modal reasoning to propositional reasoning.

Learning Implicitly with Noisy Data in Linear Arithmetic

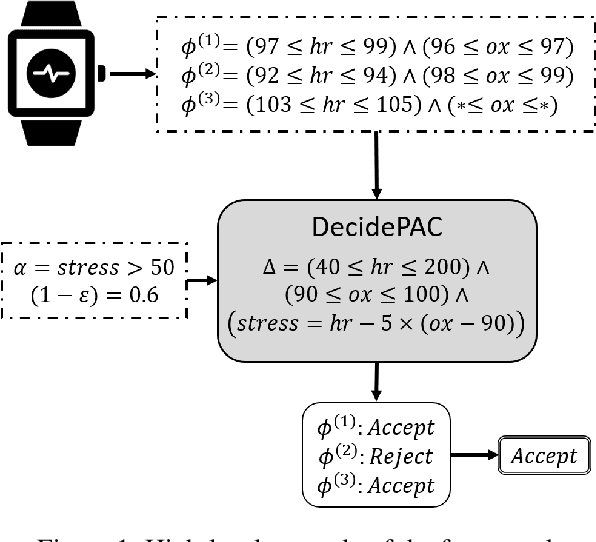
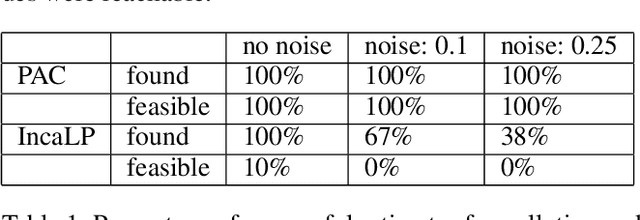
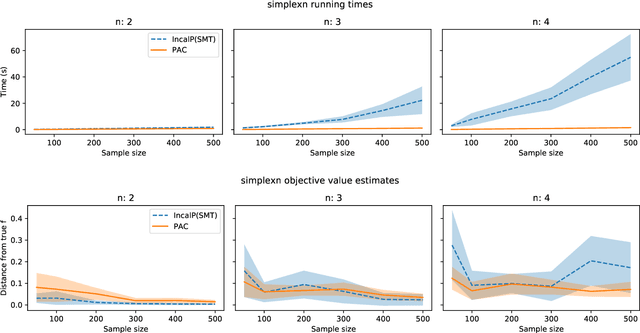
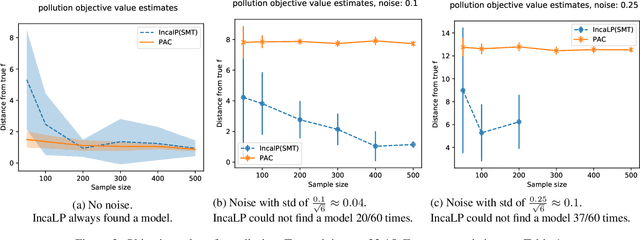
Robustly learning in expressive languages with real-world data continues to be a challenging task. Numerous conventional methods appeal to heuristics without any assurances of robustness. While PAC-Semantics offers strong guarantees, learning explicit representations is not tractable even in a propositional setting. However, recent work on so-called "implicit" learning has shown tremendous promise in terms of obtaining polynomial-time results for fragments of first-order logic. In this work, we extend implicit learning in PAC-Semantics to handle noisy data in the form of intervals and threshold uncertainty in the language of linear arithmetic. We prove that our extended framework keeps the existing polynomial-time complexity guarantees. Furthermore, we provide the first empirical investigation of this hitherto purely theoretical framework. Using benchmark problems, we show that our implicit approach to learning optimal linear programming objective constraints significantly outperforms an explicit approach in practice.