Scalable and Distributed Silhouette Approximation

The silhouette is one of the most widely used measures to assess the quality of a $k$-clustering of a dataset of $n$ elements. Its evaluation requires no information beyond the clustering assignment. In addition, the silhouette is extremely easy to interpret, providing a score to measure the quality of a clustering as a whole or for each element. The exact computation of the: (i) silhouette of each element of a dataset; and (ii) the global silhouette of the clustering; require $Θ(n^2)$ distance calculations, under general metrics. The quadratic complexity $Θ(n^2)$ is extremely prohibitive, especially on massive modern datasets. Surprisingly, existing approximate methods using $O(n^2)$ distance calculations are heuristics not offering provable and controllable guarantees on the quality of their results. We introduce the first rigorous and efficient algorithms to estimate: (i) the (local) silhouette of each element of a dataset; and (ii) the (global) silhouette; of any metric $k$-clustering. Our methods, based on sampling, perform $O(nk\varepsilon^{-2}\ln (nk/δ))$ distance computations, and provide estimates with additive error $O(\varepsilon)$ with probability at least $1-δ$. That is, parameters $\varepsilon$ and $δ$ in $(0,1)$ control the trade-off between accuracy and efficiency. We also introduce a scalable and distributed design of our methods for the MapReduce and Massively Parallel Computing (MPC) frameworks. Our distributed algorithms use a constant number of rounds and sublinear local memory. Finally, we perform extensive experiments against state-of-the-art approaches. The results show that our new techniques yield the best trade-off between accuracy and efficiency for both local and global silhouette estimation. In addition, our methods scale efficiently to massive datasets for which an exact computation of the silhouette is not practical.

Efficient Approximate Temporal Triangle Counting in Streaming with Predictions

Triangle counting is a fundamental and widely studied problem on static graphs, and recently on temporal graphs, where edges carry information on the timings of the associated events. Streaming processing and resource efficiency are crucial requirements for counting triangles in modern massive temporal graphs, with millions of nodes and up to billions of temporal edges. However, current exact and approximate algorithms are unable to handle large-scale temporal graphs. To fill such a gap, we introduce STEP, a scalable and efficient algorithm to approximate temporal triangle counts from a stream of temporal edges. STEP combines predictions to the number of triangles a temporal edge is involved in, with a simple sampling strategy, leading to scalability, efficiency, and accurate approximation of all eight temporal triangle types simultaneously. We analytically prove that, by using a sublinear amount of memory, STEP obtains unbiased and very accurate estimates. In fact, even noisy predictions can significantly reduce the variance of STEP's estimates. Our extensive experiments on massive temporal graphs with up to billions of edges demonstrate that STEP outputs high-quality estimates and is more efficient than state-of-the-art methods.

ONBRA: Rigorous Estimation of the Temporal Betweenness Centrality in Temporal Networks

In network analysis, the betweenness centrality of a node informally captures the fraction of shortest paths visiting that node. The computation of the betweenness centrality measure is a fundamental task in the analysis of modern networks, enabling the identification of the most central nodes in such networks. Additionally to being massive, modern networks also contain information about the time at which their events occur. Such networks are often called temporal networks. The temporal information makes the study of the betweenness centrality in temporal networks (i.e., temporal betweenness centrality) much more challenging than in static networks (i.e., networks without temporal information). Moreover, the exact computation of the temporal betweenness centrality is often impractical on even moderately-sized networks, given its extremely high computational cost. A natural approach to reduce such computational cost is to obtain high-quality estimates of the exact values of the temporal betweenness centrality. In this work we present ONBRA, the first sampling-based approximation algorithm for estimating the temporal betweenness centrality values of the nodes in a temporal network, providing rigorous probabilistic guarantees on the quality of its output. ONBRA is able to compute the estimates of the temporal betweenness centrality values under two different optimality criteria for the shortest paths of the temporal network. In addition, ONBRA outputs high-quality estimates with sharp theoretical guarantees leveraging on the \emph{empirical Bernstein bound}, an advanced concentration inequality. Finally, our experimental evaluation shows that ONBRA significantly reduces the computational resources required by the exact computation of the temporal betweenness centrality on several real world networks, while reporting high-quality estimates with rigorous guarantees.

odeN: Simultaneous Approximation of Multiple Motif Counts in Large Temporal Networks

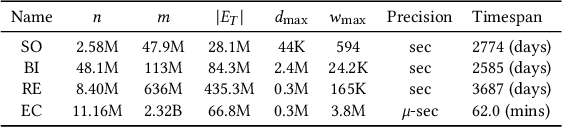
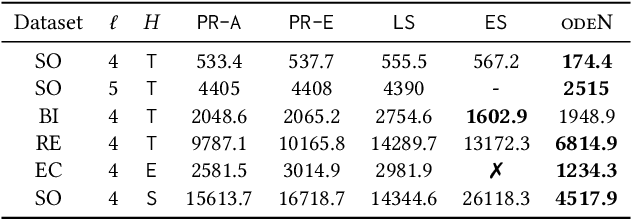
Counting the number of occurrences of small connected subgraphs, called temporal motifs, has become a fundamental primitive for the analysis of temporal networks, whose edges are annotated with the time of the event they represent. One of the main complications in studying temporal motifs is the large number of motifs that can be built even with a limited number of vertices or edges. As a consequence, since in many applications motifs are employed for exploratory analyses, the user needs to iteratively select and analyze several motifs that represent different aspects of the network, resulting in an inefficient, time-consuming process. This problem is exacerbated in large networks, where the analysis of even a single motif is computationally demanding. As a solution, in this work we propose and study the problem of simultaneously counting the number of occurrences of multiple temporal motifs, all corresponding to the same (static) topology (e.g., a triangle). Given that for large temporal networks computing the exact counts is unfeasible, we propose odeN, a sampling-based algorithm that provides an accurate approximation of all the counts of the motifs. We provide analytical bounds on the number of samples required by odeN to compute rigorous, probabilistic, relative approximations. Our extensive experimental evaluation shows that odeN enables the approximation of the counts of motifs in temporal networks in a fraction of the time needed by state-of-the-art methods, and that it also reports more accurate approximations than such methods.

PRESTO: Simple and Scalable Sampling Techniques for the Rigorous Approximation of Temporal Motif Counts

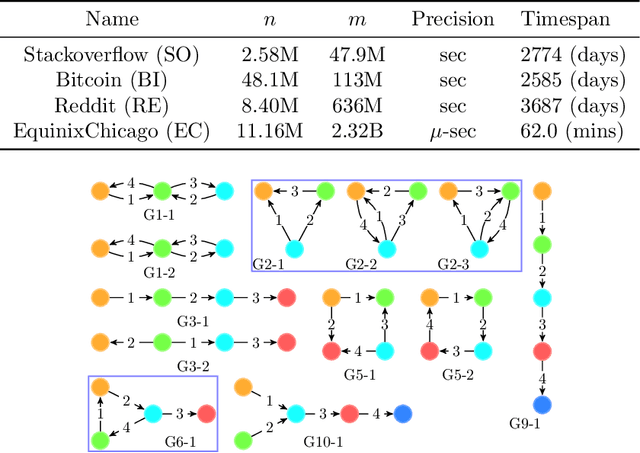
The identification and counting of small graph patterns, called network motifs, is a fundamental primitive in the analysis of networks, with application in various domains, from social networks to neuroscience. Several techniques have been designed to count the occurrences of motifs in static networks, with recent work focusing on the computational challenges provided by large networks. Modern networked datasets contain rich information, such as the time at which the events modeled by the networks edges happened, which can provide useful insights into the process modeled by the network. The analysis of motifs in temporal networks, called temporal motifs, is becoming an important component in the analysis of modern networked datasets. Several methods have been recently designed to count the number of instances of temporal motifs in temporal networks, which is even more challenging than its counterpart for static networks. Such methods are either exact, and not applicable to large networks, or approximate, but provide only weak guarantees on the estimates they produce and do not scale to very large networks. In this work we present an efficient and scalable algorithm to obtain rigorous approximations of the count of temporal motifs. Our algorithm is based on a simple but effective sampling approach, which renders our algorithm practical for very large datasets. Our extensive experimental evaluation shows that our algorithm provides estimates of temporal motif counts which are more accurate than the state-of-the-art sampling algorithms, with significantly lower running time than exact approaches, enabling the study of temporal motifs, of size larger than the ones considered in previous works, on billion edges networks.