Hyungsuk Tak
Repelling-Attracting Hamiltonian Monte Carlo
Mar 07, 2024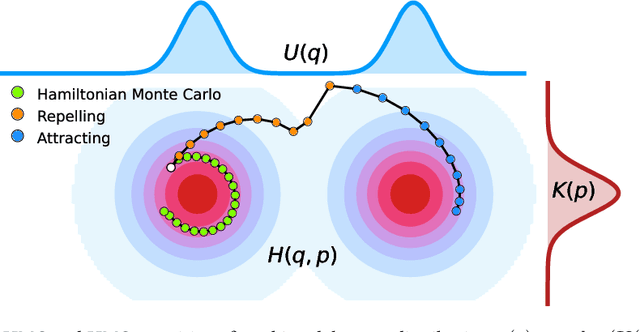

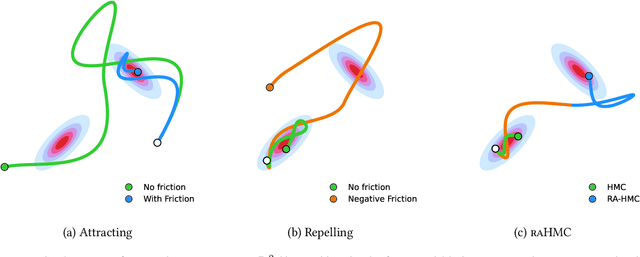
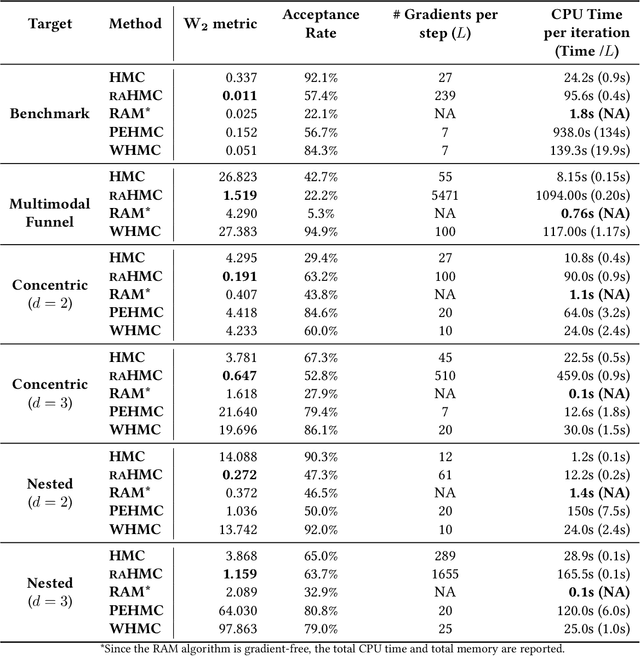
Abstract:We propose a variant of Hamiltonian Monte Carlo (HMC), called the Repelling-Attracting Hamiltonian Monte Carlo (RAHMC), for sampling from multimodal distributions. The key idea that underpins RAHMC is a departure from the conservative dynamics of Hamiltonian systems, which form the basis of traditional HMC, and turning instead to the dissipative dynamics of conformal Hamiltonian systems. In particular, RAHMC involves two stages: a mode-repelling stage to encourage the sampler to move away from regions of high probability density; and, a mode-attracting stage, which facilitates the sampler to find and settle near alternative modes. We achieve this by introducing just one additional tuning parameter -- the coefficient of friction. The proposed method adapts to the geometry of the target distribution, e.g., modes and density ridges, and can generate proposals that cross low-probability barriers with little to no computational overhead in comparison to traditional HMC. Notably, RAHMC requires no additional information about the target distribution or memory of previously visited modes. We establish the theoretical basis for RAHMC, and we discuss repelling-attracting extensions to several variants of HMC in literature. Finally, we provide a tuning-free implementation via dual-averaging, and we demonstrate its effectiveness in sampling from, both, multimodal and unimodal distributions in high dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge