Heuristic Modularity Maximization Algorithms for Community Detection Rarely Return an Optimal Partition or Anything Similar

Community detection is a classic problem in network science with extensive applications in various fields. The most commonly used methods are the algorithms designed to maximize modularity over different partitions of the network nodes into communities. Using 80 real and random networks from a wide range of contexts, we investigate the extent to which current heuristic modularity maximization algorithms succeed in returning modularity-maximum (optimal) partitions. We evaluate (1) the ratio of their output modularity to the maximum modularity for each input graph and (2) the maximum similarity between their output partition and any optimal partition of that graph. Our computational experiments involve eight existing heuristic algorithms which we compare against an exact integer programming method that globally maximizes modularity. The average modularity-based heuristic algorithm returns optimal partitions for only 16.9% of the 80 graphs considered. Results on adjusted mutual information show considerable dissimilarity between the sub-optimal partitions and any optimal partitions of the graphs in our experiments. More importantly, our results show that near-optimal partitions tend to be disproportionally dissimilar to any optimal partition. Taken together, our analysis points to a crucial limitation of commonly used modularity-based algorithms for discovering communities: they rarely return an optimal partition or a partition resembling an optimal partition. Given this finding, developing an exact or approximate algorithm for modularity maximization is recommendable for a more methodologically sound usage of modularity in community detection.

The Bayan Algorithm: Detecting Communities in Networks Through Exact and Approximate Optimization of Modularity

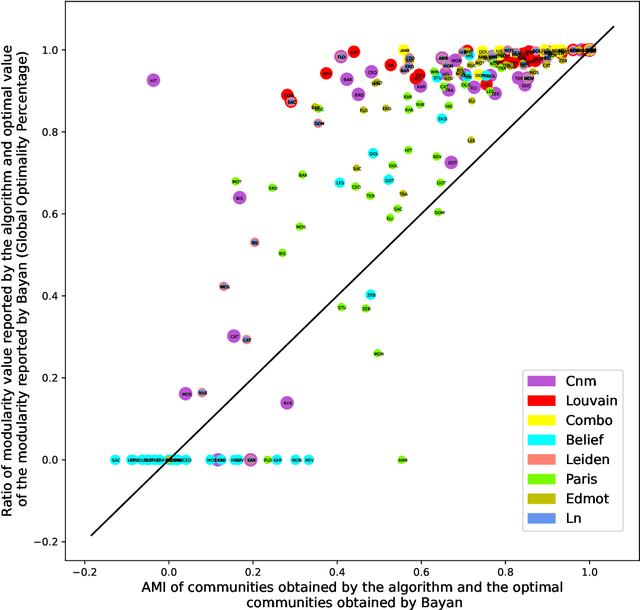
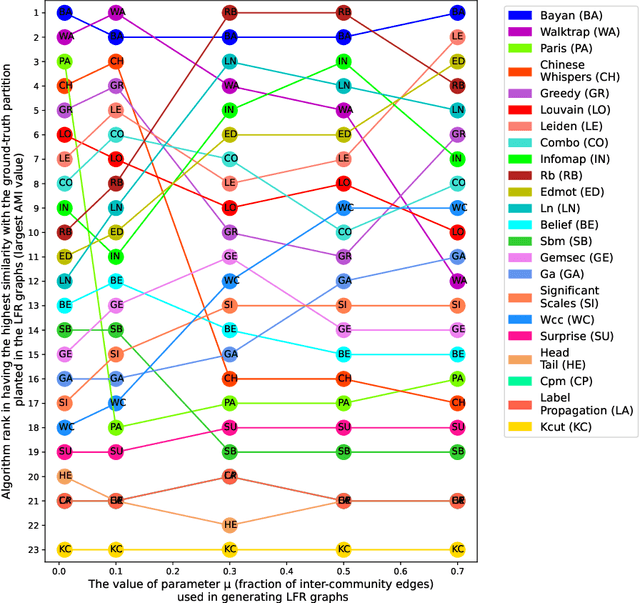
Community detection is a classic problem in network science with extensive applications in various fields. The most commonly used methods are the algorithms designed to maximize a utility function, modularity, across different ways that a network can be partitioned into communities. Despite their name and design philosophy, current modularity maximization algorithms generally fail to maximize modularity or guarantee any proximity to an optimal solution. We propose the Bayan algorithm which, unlike the existing methods, returns network partitions with a guarantee of either optimality or proximity to an optimal solution. At the core of the Bayan algorithm is a branch-and-cut scheme that solves a sparse integer programming formulation of the modularity maximization problem to optimality or approximate it within a factor. We analyze the performance of Bayan against 22 existing algorithms using synthetic and real networks. Through extensive experiments, we demonstrate Bayan's distinctive capabilities not only in maximizing modularity, but more importantly in accurate retrieval of ground-truth communities. Bayan's comparative level of performance remains stable over variations in the amount of noise in the data (graph) generation process. The performance of Bayan as an exact modularity maximization algorithm also reveals the theoretical capability limits of maximum-modularity partitions in accurate retrieval of communities. Overall our analysis points to Bayan as a suitable choice for a methodologically grounded detection of communities through exact (approximate) maximization of modularity in networks with up to $\sim10^3$ edges (and larger networks). Prospective advances in graph optimization and integer programming can push these limits further.