Learning-based Adaptive Control of Quadruped Robots for Active Stabilization on Moving Platforms

A quadruped robot faces balancing challenges on a six-degrees-of-freedom moving platform, like subways, buses, airplanes, and yachts, due to independent platform motions and resultant diverse inertia forces on the robot. To alleviate these challenges, we present the Learning-based Active Stabilization on Moving Platforms (\textit{LAS-MP}), featuring a self-balancing policy and system state estimators. The policy adaptively adjusts the robot's posture in response to the platform's motion. The estimators infer robot and platform states based on proprioceptive sensor data. For a systematic training scheme across various platform motions, we introduce platform trajectory generation and scheduling methods. Our evaluation demonstrates superior balancing performance across multiple metrics compared to three baselines. Furthermore, we conduct a detailed analysis of the \textit{LAS-MP}, including ablation studies and evaluation of the estimators, to validate the effectiveness of each component.

TORM: Collision-Free Trajectory Optimization of Redundant Manipulator given an End-Effector Path

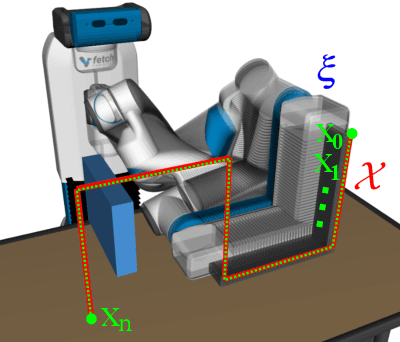
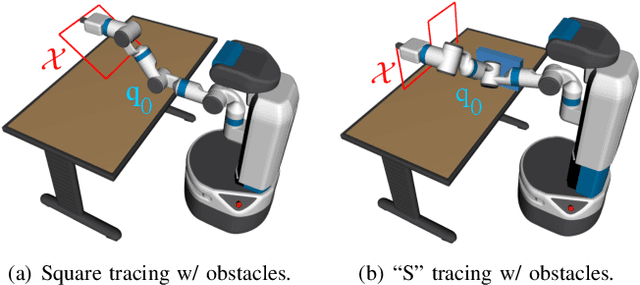
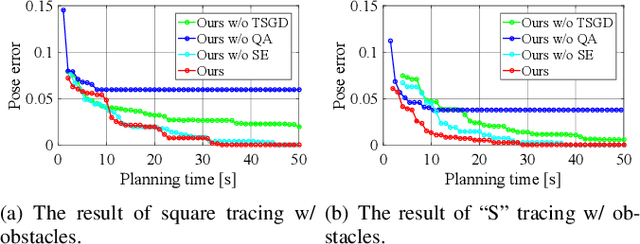
A redundant manipulator has multiple inverse kinematics solutions per an end-effector pose. Accordingly, there can be many trajectories for joints that follow a given end-effector path in a Cartesian space. In this paper, we present a trajectory optimization of a redundant manipulator (TORM) to synthesize a trajectory that follows a given end-effector path accurately, while achieving the smoothness and collision-free manipulation. Given these desirable properties, our method optimizes a trajectory using two-stage gradient descent to reduce potential competition between different properties during the update. To further improve the performance and avoid falling into local minima, we apply the quantum annealing that iteratively randomizes various configurations of the trajectory, followed by updating the trajectory. We first show benefits of our method with environments containing external obstacles. We then compare ours with the state-of-the-art methods in their favorable setting, environments without having obstacles. Our method robustly minimizes the pose error in a progressive manner while satisfying various desirable properties.