Han Lin Shang
Detection and Estimation of Structural Breaks in High-Dimensional Functional Time Series
Apr 14, 2023
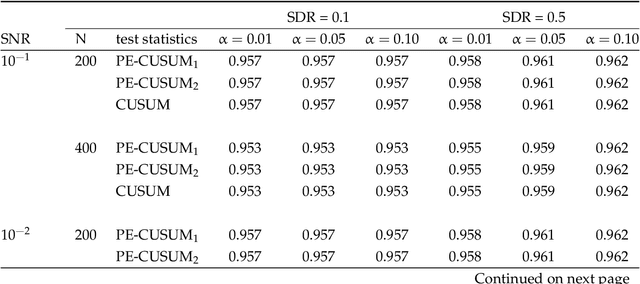


Abstract:In this paper, we consider detecting and estimating breaks in heterogeneous mean functions of high-dimensional functional time series which are allowed to be cross-sectionally correlated and temporally dependent. A new test statistic combining the functional CUSUM statistic and power enhancement component is proposed with asymptotic null distribution theory comparable to the conventional CUSUM theory derived for a single functional time series. In particular, the extra power enhancement component enlarges the region where the proposed test has power, and results in stable power performance when breaks are sparse in the alternative hypothesis. Furthermore, we impose a latent group structure on the subjects with heterogeneous break points and introduce an easy-to-implement clustering algorithm with an information criterion to consistently estimate the unknown group number and membership. The estimated group structure can subsequently improve the convergence property of the post-clustering break point estimate. Monte-Carlo simulation studies and empirical applications show that the proposed estimation and testing techniques have satisfactory performance in finite samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge