H. Haddad Khodaparast
Fuzzy finite element model updating using metaheuristic optimization algorithms
Jan 03, 2017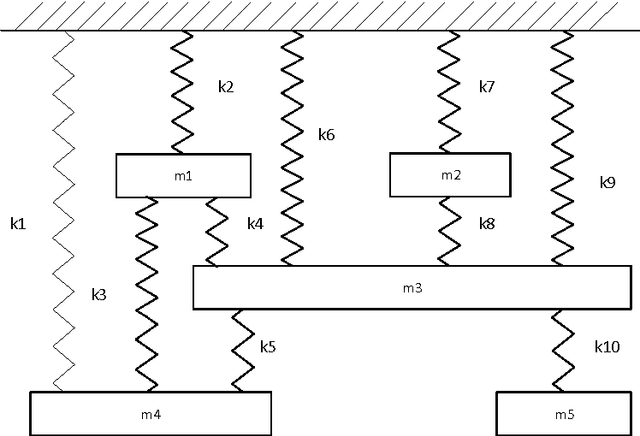
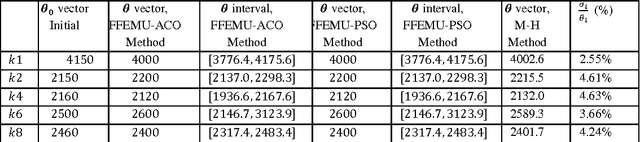
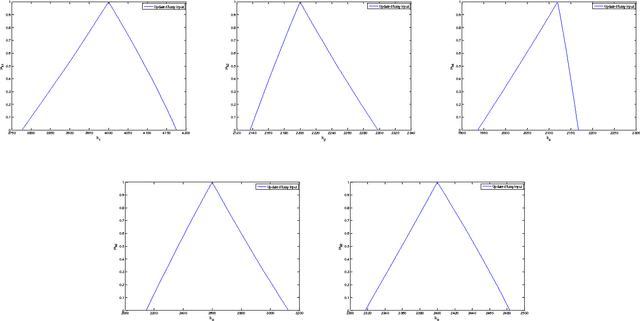
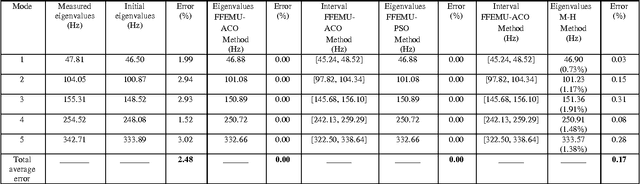
Abstract:In this paper, a non-probabilistic method based on fuzzy logic is used to update finite element models (FEMs). Model updating techniques use the measured data to improve the accuracy of numerical models of structures. However, the measured data are contaminated with experimental noise and the models are inaccurate due to randomness in the parameters. This kind of aleatory uncertainty is irreducible, and may decrease the accuracy of the finite element model updating process. However, uncertainty quantification methods can be used to identify the uncertainty in the updating parameters. In this paper, the uncertainties associated with the modal parameters are defined as fuzzy membership functions, while the model updating procedure is defined as an optimization problem at each {\alpha}-cut level. To determine the membership functions of the updated parameters, an objective function is defined and minimized using two metaheuristic optimization algorithms: ant colony optimization (ACO) and particle swarm optimization (PSO). A structural example is used to investigate the accuracy of the fuzzy model updating strategy using the PSO and ACO algorithms. Furthermore, the results obtained by the fuzzy finite element model updating are compared with the Bayesian model updating results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge