InVAErt networks for amortized inference and identifiability analysis of lumped parameter hemodynamic models

Estimation of cardiovascular model parameters from electronic health records (EHR) poses a significant challenge primarily due to lack of identifiability. Structural non-identifiability arises when a manifold in the space of parameters is mapped to a common output, while practical non-identifiability can result due to limited data, model misspecification, or noise corruption. To address the resulting ill-posed inverse problem, optimization-based or Bayesian inference approaches typically use regularization, thereby limiting the possibility of discovering multiple solutions. In this study, we use inVAErt networks, a neural network-based, data-driven framework for enhanced digital twin analysis of stiff dynamical systems. We demonstrate the flexibility and effectiveness of inVAErt networks in the context of physiological inversion of a six-compartment lumped parameter hemodynamic model from synthetic data to real data with missing components.

InVAErt networks: a data-driven framework for emulation, inference and identifiability analysis

Use of generative models and deep learning for physics-based systems is currently dominated by the task of emulation. However, the remarkable flexibility offered by data-driven architectures would suggest to extend this representation to other aspects of system synthesis including model inversion and identifiability. We introduce inVAErt (pronounced \emph{invert}) networks, a comprehensive framework for data-driven analysis and synthesis of parametric physical systems which uses a deterministic encoder and decoder to represent the forward and inverse solution maps, normalizing flow to capture the probabilistic distribution of system outputs, and a variational encoder designed to learn a compact latent representation for the lack of bijectivity between inputs and outputs. We formally investigate the selection of penalty coefficients in the loss function and strategies for latent space sampling, since we find that these significantly affect both training and testing performance. We validate our framework through extensive numerical examples, including simple linear, nonlinear, and periodic maps, dynamical systems, and spatio-temporal PDEs.

Data-driven synchronization-avoiding algorithms in the explicit distributed structural analysis of soft tissue

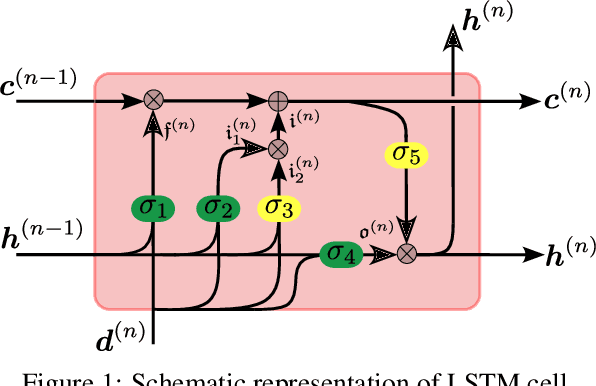
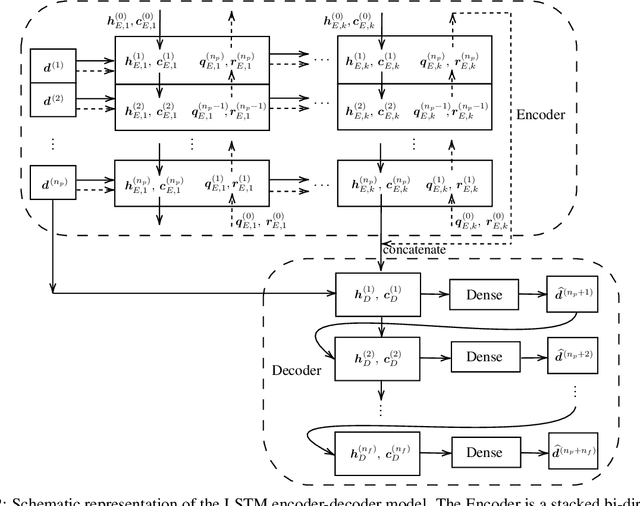
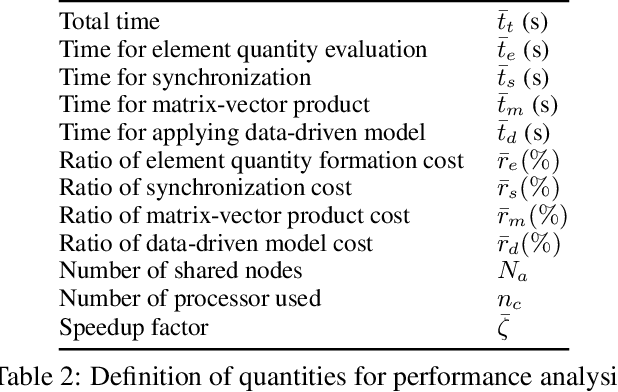
We propose a data-driven framework to increase the computational efficiency of the explicit finite element method in the structural analysis of soft tissue. An encoder-decoder long short-term memory deep neural network is trained based on the data produced by an explicit, distributed finite element solver. We leverage this network to predict synchronized displacements at shared nodes, minimizing the amount of communication between processors. We perform extensive numerical experiments to quantify the accuracy and stability of the proposed synchronization-avoiding algorithm.