Gokcen Buyukbas
Rehabilitating Isomap: Euclidean Representation of Geodesic Structure
Jun 18, 2020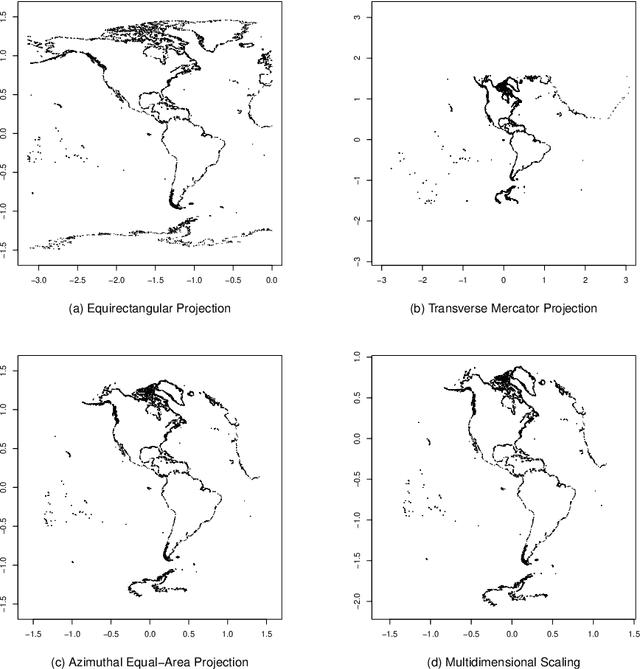
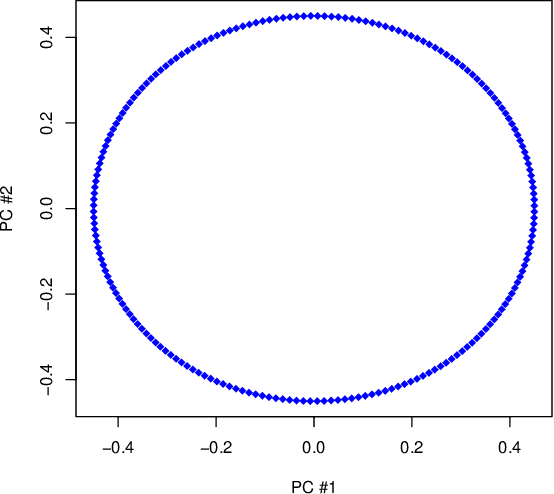
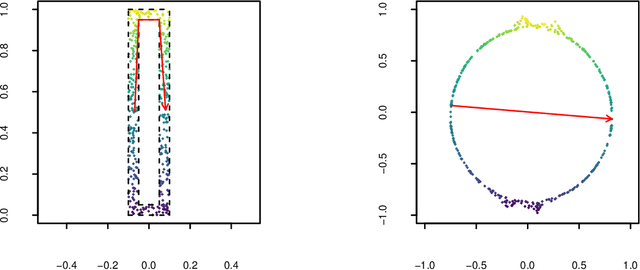
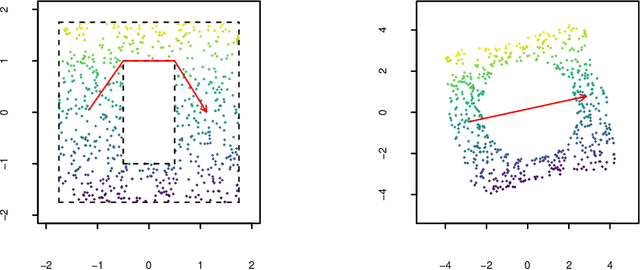
Abstract:Manifold learning techniques for nonlinear dimension reduction assume that high-dimensional feature vectors lie on a low-dimensional manifold, then attempt to exploit manifold structure to obtain useful low-dimensional Euclidean representations of the data. Isomap, a seminal manifold learning technique, is an elegant synthesis of two simple ideas: the approximation of Riemannian distances with shortest path distances on a graph that localizes manifold structure, and the approximation of shortest path distances with Euclidean distances by multidimensional scaling. We revisit the rationale for Isomap, clarifying what Isomap does and what it does not. In particular, we explore the widespread perception that Isomap should only be used when the manifold is parametrized by a convex region of Euclidean space. We argue that this perception is based on an extremely narrow interpretation of manifold learning as parametrization recovery, and we submit that Isomap is better understood as constructing Euclidean representations of geodesic structure. We reconsider a well-known example that was previously interpreted as evidence of Isomap's limitations, and we re-examine the original analysis of Isomap's convergence properties, concluding that convexity is not required for shortest path distances to converge to Riemannian distances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge