Data-driven uncertainty-aware seakeeping prediction of the Delft 372 catamaran using ensemble Hankel dynamic mode decomposition

In this study, we present and validate an ensemble-based Hankel Dynamic Mode Decomposition with control (HDMDc) for uncertainty-aware seakeeping predictions of a high-speed catamaran, namely the Delft 372 model. Experimental measurements (time histories) of wave elevation at the longitudinal center of gravity, heave, pitch, notional flight-deck velocity, notional bridge acceleration, and total resistance were collected from irregular wave basin tests on a 1:33.3 scale replica of the Delft 372 model under sea state 5 conditions at Fr = 0.425, and organized into training, validation, and test sets. The HDMDc algorithm constructs an equation-free linear reduced-order model of the seakeeping vessel by augmenting states and inputs with their time-lagged copies to capture nonlinear and memory effects. Two ensembling strategies, namely Bayesian HDMDc (BHDMDc), which samples hyperparameters considered stochastic variables with prior distribution to produce posterior mean forecasts with confidence intervals, and Frequentist HDMDc (FHDMDc), which aggregates multiple model obtained over data subsets, are compared in providing seakeeping prediction and uncertainty quantification. The FHDMDc approach is found to improve the accuracy of the predictions compared to the deterministic counterpart, also providing robust uncertainty estimation; whereas the application of BHDMDc to the present test case is not found beneficial in comparison to the deterministic model. FHDMDc-derived probability density functions for the motions closely match both experimental data and URANS results, demonstrating reliable and computationally efficient seakeeping prediction for design and operational support.

System Identification of a Moored ASV with Recessed Moon Pool via Deterministic and Bayesian Hankel-DMDc

This study addresses the system identification of a small autonomous surface vehicle (ASV) under moored conditions using Hankel dynamic mode decomposition with control (HDMDc) and its Bayesian extension (BHDMDc). Experiments were carried out on a Codevintec CK-14e ASV in the towing tank of CNR-INM, under both irregular and regular head-sea wave conditions. The ASV under investigation features a recessed moon pool, which induces nonlinear responses due to sloshing, thereby increasing the modelling challenge. Data-driven reduced-order models were built from measurements of vessel motions and mooring loads. The HDMDc framework provided accurate deterministic predictions of vessel dynamics, while the Bayesian formulation enabled uncertainty-aware characterization of the model response by accounting for variability in hyperparameter selection. Validation against experimental data demonstrated that both HDMDc and BHDMDc can predict the vessel's response to unseen regular and irregular wave excitations. In conclusion, the study shows that HDMDc-based ROMs are a viable data-driven alternative for system identification, demonstrating for the first time their generalization capability for a sea condition different from the training set, achieving high accuracy in reproducing vessel dynamics.

Bayesian dynamic mode decomposition for real-time ship motion digital twinning

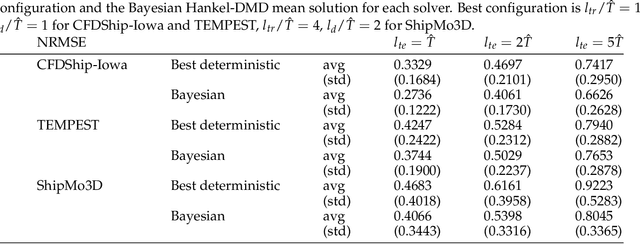
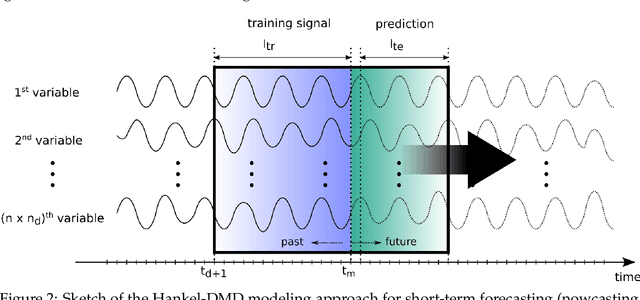
Digital twins are widely considered enablers of groundbreaking changes in the development, operation, and maintenance of novel generations of products. They are meant to provide reliable and timely predictions to inform decisions along the entire product life cycle. One of their most interesting applications in the naval field is the digital twinning of ship performances in waves, a crucial aspect in design and operation safety. In this paper, a Bayesian extension of the Hankel dynamic mode decomposition method is proposed for ship motion's nowcasting as a prediction tool for naval digital twins. The proposed algorithm meets all the requirements for formulations devoted to digital twinning, being able to adapt the resulting models with the data incoming from the physical system, using a limited amount of data, producing real-time predictions, and estimating their reliability. Results are presented and discussed for the course-keeping of the 5415M model in beam-quartering sea state 7 irregular waves at Fr = 0.33, using data from three different CFD solvers. The results show predictions keeping good accuracy levels up to five wave encounter periods, with the Bayesian formulation improving the deterministic forecasts. In addition, a connection between the predicted uncertainty and prediction accuracy is found.

Analysis and Forecasting of the Dynamics of a Floating Wind Turbine Using Dynamic Mode Decomposition

This article presents a data-driven equation-free modeling of the dynamics of a hexafloat floating offshore wind turbine based on the Dynamic Mode Decomposition (DMD). The DMD is here used to provide a modal analysis and extract knowledge from the dynamic system. A forecasting algorithm for the motions, accelerations, and forces acting on the floating system, as well as the height of the incoming waves, the wind speed, and the power extracted by the wind turbine, is developed by using a methodological extension called Hankel-DMD, that includes time-delayed copies of the states in an augmented state vector. All the analyses are performed on experimental data collected from an operating prototype. The quality of the forecasts obtained varying two main hyperparameters of the algorithm, namely the number of delayed copies and the length of the observation time, is assessed using three different error metrics, each analyzing complementary aspects of the prediction. A statistical analysis exposed the existence of optimal values for the algorithm hyperparameters. Results show the approach's capability for short-term future estimates of the system's state, which can be used for real-time prediction and control. Furthermore, a novel Stochastic Hankel-DMD formulation is introduced by considering hyperparameters as stochastic variables. The stochastic version of the method not only enriches the prediction with its related uncertainty but is also found to improve the normalized root mean square error up to 10% on a statistical basis compared to the deterministic counterpart.