Synergistic pathways of modulation enable robust task packing within neural dynamics

Understanding how brain networks learn and manage multiple tasks simultaneously is of interest in both neuroscience and artificial intelligence. In this regard, a recent research thread in theoretical neuroscience has focused on how recurrent neural network models and their internal dynamics enact multi-task learning. To manage different tasks requires a mechanism to convey information about task identity or context into the model, which from a biological perspective may involve mechanisms of neuromodulation. In this study, we use recurrent network models to probe the distinctions between two forms of contextual modulation of neural dynamics, at the level of neuronal excitability and at the level of synaptic strength. We characterize these mechanisms in terms of their functional outcomes, focusing on their robustness to context ambiguity and, relatedly, their efficiency with respect to packing multiple tasks into finite size networks. We also demonstrate distinction between these mechanisms at the level of the neuronal dynamics they induce. Together, these characterizations indicate complementarity and synergy in how these mechanisms act, potentially over multiple time-scales, toward enhancing robustness of multi-task learning.

DFORM: Diffeomorphic vector field alignment for assessing dynamics across learned models

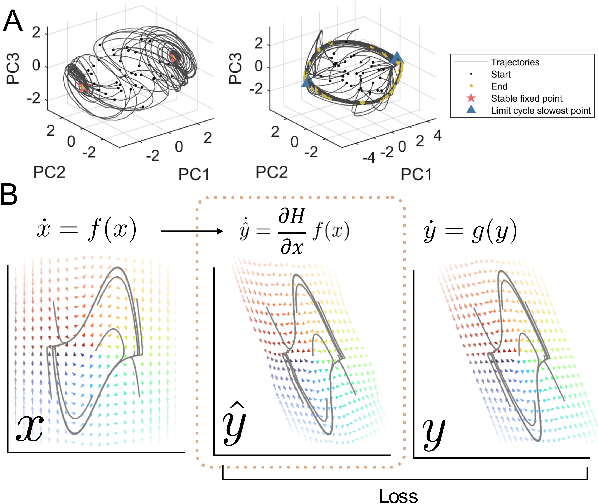
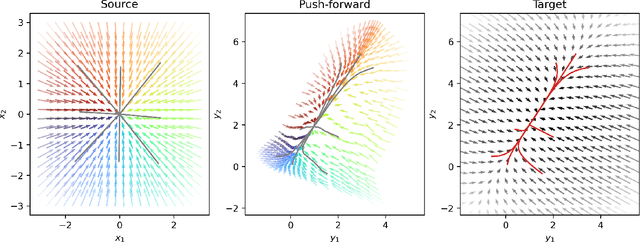
Dynamical system models such as Recurrent Neural Networks (RNNs) have become increasingly popular as hypothesis-generating tools in scientific research. Evaluating the dynamics in such networks is key to understanding their learned generative mechanisms. However, comparison of learned dynamics across models is challenging due to their inherent nonlinearity and because a priori there is no enforced equivalence of their coordinate systems. Here, we propose the DFORM (Diffeomorphic vector field alignment for comparing dynamics across learned models) framework. DFORM learns a nonlinear coordinate transformation which provides a continuous, maximally one-to-one mapping between the trajectories of learned models, thus approximating a diffeomorphism between them. The mismatch between DFORM-transformed vector fields defines the orbital similarity between two models, thus providing a generalization of the concepts of smooth orbital and topological equivalence. As an example, we apply DFORM to models trained on a canonical neuroscience task, showing that learned dynamics may be functionally similar, despite overt differences in attractor landscapes.