Approximate Environment Decompositions for Robot Coverage Planning using Submodular Set Cover

In this paper, we investigate the problem of decomposing 2D environments for robot coverage planning. Coverage path planning (CPP) involves computing a cost-minimizing path for a robot equipped with a coverage or sensing tool so that the tool visits all points in the environment. CPP is an NP-Hard problem, so existing approaches simplify the problem by decomposing the environment into the minimum number of sectors. Sectors are sub-regions of the environment that can each be covered using a lawnmower path (i.e., along parallel straight-line paths) oriented at an angle. However, traditional methods either limit the coverage orientations to be axis-parallel (horizontal/vertical) or provide no guarantees on the number of sectors in the decomposition. We introduce an approach to decompose the environment into possibly overlapping rectangular sectors. We provide an approximation guarantee on the number of sectors computed using our approach for a given environment. We do this by leveraging the submodular property of the sector coverage function, which enables us to formulate the decomposition problem as a submodular set cover (SSC) problem with well-known approximation guarantees for the greedy algorithm. Our approach improves upon existing coverage planning methods, as demonstrated through an evaluation using maps of complex real-world environments.

Anytime Replanning of Robot Coverage Paths for Partially Unknown Environments

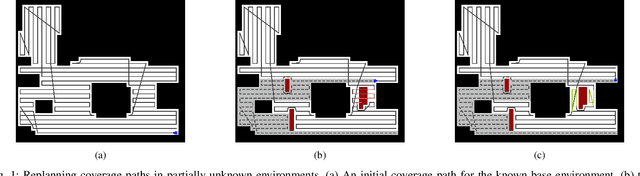
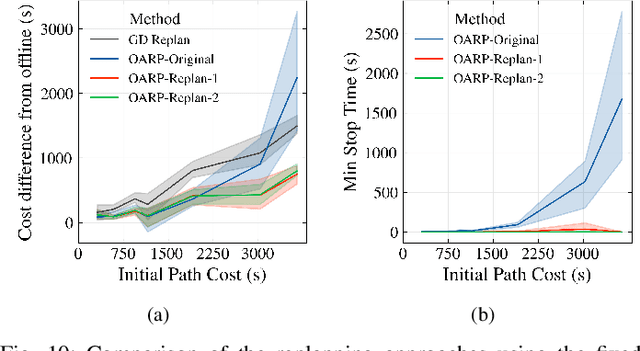
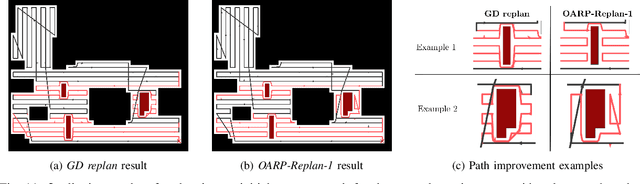
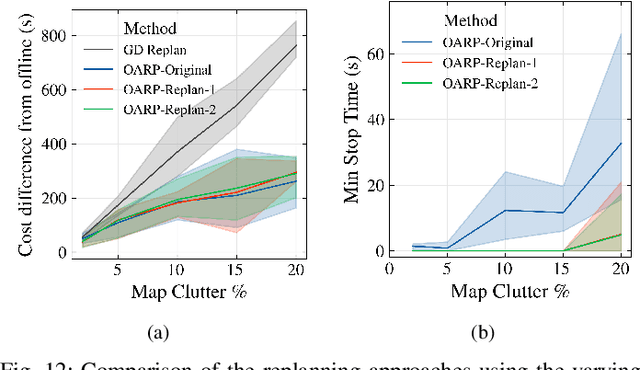
In this paper, we propose a method to replan coverage paths for a robot operating in an environment with initially unknown static obstacles. Existing coverage approaches reduce coverage time by covering along the minimum number of coverage lines (straight-line paths). However, recomputing such paths online can be computationally expensive resulting in robot stoppages that increase coverage time. A naive alternative is greedy detour replanning, i.e., replanning with minimum deviation from the initial path, which is efficient to compute but may result in unnecessary detours. In this work, we propose an anytime coverage replanning approach named OARP-Replan that performs near-optimal replans to an interrupted coverage path within a given time budget. We do this by solving linear relaxations of mixed-integer linear programs (MILPs) to identify sections of the interrupted path that can be optimally replanned within the time budget. We validate our approach in simulation using maps of real-world environments and compare our approach against a greedy detour replanner and other state-of-the-art approaches.

Optimal Partitioning of Non-Convex Environments for Minimum Turn Coverage Planning

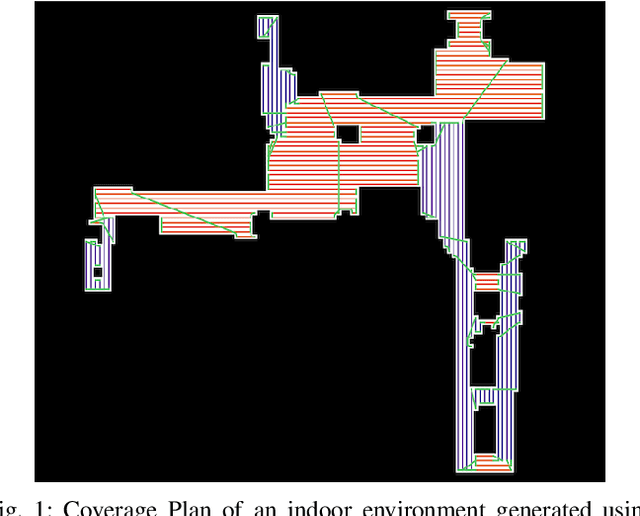
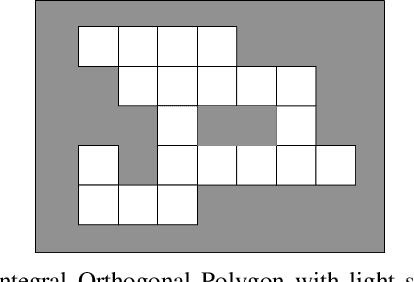
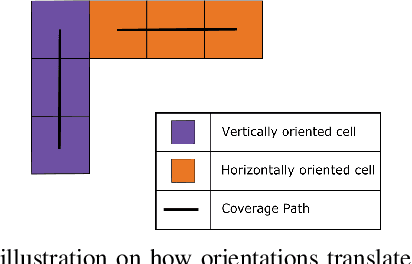
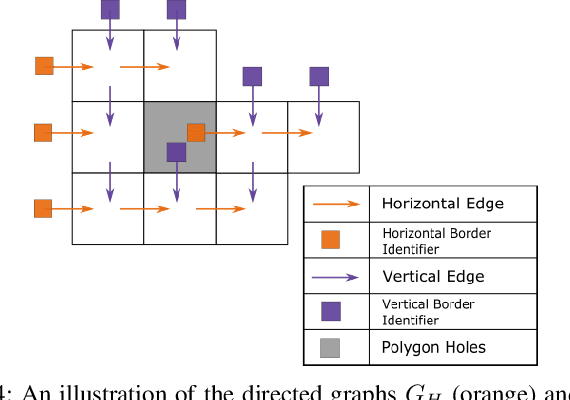
In this paper, we tackle the problem of generating a turn-minimizing coverage plan for a robot operating in an indoor environment. In coverage planning, the number of turns in the generated path affects the time to cover the environment and the quality of coverage, e.g. tools like cameras and cleaning attachments commonly have poor performance around turns. In many existing turn-minimizing coverage methods, the environment is partitioned into the least number of ranks, which are non-intersecting rectangles of width equal to the robot's tool width. This partitioning problem is typically solved using heuristics that do not guarantee optimality. In this work, we propose a linear programming (LP) approach to partition the environment into the least number of axis-parallel (horizontal and vertical) ranks with the goal of minimizing the number of turns taken by the robot. We prove that our LP method solves this problem optimally and in polynomial time. We then generate coverage plans for a set of indoor environments using the proposed LP method and compare the results against that of a state-of-the-art coverage approach.

Clustering in Discrete Path Planning for Approximating Minimum Length Paths

In this paper we consider discrete robot path planning problems on metric graphs. We propose a clustering method, Gamma-Clustering for the planning graph that significantly reduces the number of feasible solutions, yet retains a solution within a constant factor of the optimal. By increasing the input parameter Gamma, the constant factor can be decreased, but with less reduction in the search space. We provide a simple polynomial- time algorithm for finding optimal Gamma-Clusters, and show that for a given Gamma, this optimal is unique. We demonstrate the effectiveness of the clustering method on traveling salesman instances, showing that for many instances we obtain significant reductions in computation time with little to no reduction in solution quality.