Franco Alberto Cardillo
MILP-SAT-GNN: Yet Another Neural SAT Solver
Jul 02, 2025Abstract:We proposes a novel method that enables Graph Neural Networks (GNNs) to solve SAT problems by leveraging a technique developed for applying GNNs to Mixed Integer Linear Programming (MILP). Specifically, k-CNF formulae are mapped into MILP problems, which are then encoded as weighted bipartite graphs and subsequently fed into a GNN for training and testing. From a theoretical perspective: (i) we establish permutation and equivalence invariance results, demonstrating that the method produces outputs that are stable under reordering of clauses and variables; (ii) we identify a theoretical limitation, showing that for a class of formulae called foldable formulae, standard GNNs cannot always distinguish satisfiable from unsatisfiable instances; (iii) we prove a universal approximation theorem, establishing that with Random Node Initialization (RNI), the method can approximate SAT solving to arbitrary precision on finite datasets, that is, the GNN becomes approximately sound and complete on such datasets. Furthermore, we show that for unfoldable formulae, the same approximation guarantee can be achieved without the need for RNI. Finally, we conduct an experimental evaluation of our approach, which show that, despite the simplicity of the neural architecture, the method achieves promising results.
U-NetMN and SegNetMN: Modified U-Net and SegNet models for bimodal SAR image segmentation
Jun 05, 2025Abstract:Segmenting Synthetic Aperture Radar (SAR) images is crucial for many remote sensing applications, particularly water body detection. However, deep learning-based segmentation models often face challenges related to convergence speed and stability, mainly due to the complex statistical distribution of this type of data. In this study, we evaluate the impact of mode normalization on two widely used semantic segmentation models, U-Net and SegNet. Specifically, we integrate mode normalization, to reduce convergence time while maintaining the performance of the baseline models. Experimental results demonstrate that mode normalization significantly accelerates convergence. Furthermore, cross-validation results indicate that normalized models exhibit increased stability in different zones. These findings highlight the effectiveness of normalization in improving computational efficiency and generalization in SAR image segmentation.
PN-OWL: A Two Stage Algorithm to Learn Fuzzy Concept Inclusions from OWL Ontologies
Mar 01, 2023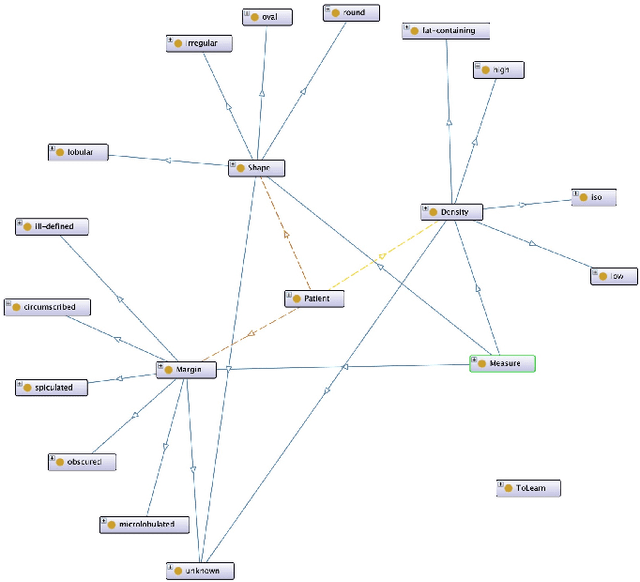

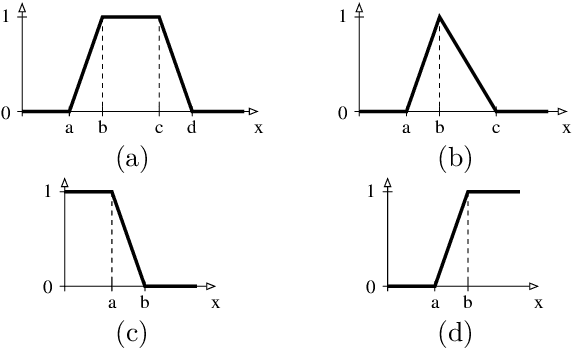
Abstract:OWL ontologies are a quite popular way to describe structured knowledge in terms of classes, relations among classes and class instances. In this paper, given a target class T of an OWL ontology, with a focus on ontologies with real- and boolean-valued data properties, we address the problem of learning graded fuzzy concept inclusion axioms with the aim of describing enough conditions for being an individual classified as instance of the class T. To do so, we present PN-OWL that is a two-stage learning algorithm made of a P-stage and an N-stage. Roughly, in the P-stage the algorithm tries to cover as many positive examples as possible (increase recall), without compromising too much precision, while in the N-stage, the algorithm tries to rule out as many false positives, covered by the P-stage, as possible. PN-OWL then aggregates the fuzzy inclusion axioms learnt at the P-stage and the N-stage by combining them via aggregation functions to allow for a final decision whether an individual is instance of T or not. We also illustrate its effectiveness by means of an experimentation. An interesting feature is that fuzzy datatypes are built automatically, the learnt fuzzy concept inclusions can be represented directly into Fuzzy OWL 2 and, thus, any Fuzzy OWL 2 reasoner can then be used to automatically determine/classify (and to which degree) whether an individual belongs to the target class T or not.
Fuzzy OWL-BOOST: Learning Fuzzy Concept Inclusions via Real-Valued Boosting
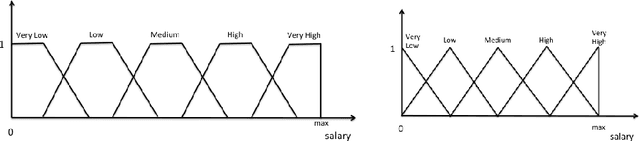
Aug 03, 2020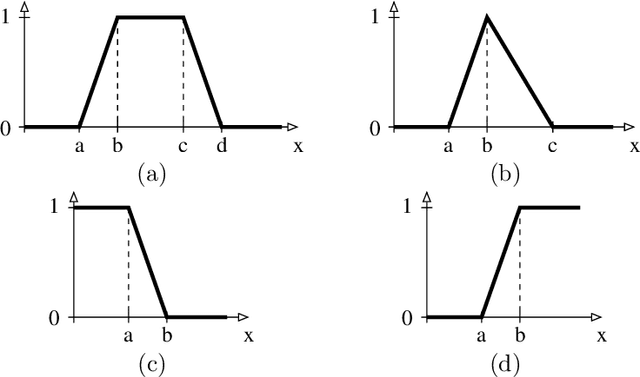

Abstract:OWL ontologies are nowadays a quite popular way to describe structured knowledge in terms of classes, relations among classes and class instances. In this paper, given a target class T of an OWL ontology, we address the problem of learning fuzzy concept inclusion axioms that describe sufficient conditions for being an individual instance of T. To do so, we present Fuzzy OWL-BOOST that relies on the Real AdaBoost boosting algorithm adapted to the (fuzzy) OWL case. We illustrate its effectiveness by means of an experimentation. An interesting feature is that the learned rules can be represented directly into Fuzzy OWL 2. As a consequence, any Fuzzy OWL 2 reasoner can then be used to automatically determine/classify (and to which degree) whether an individual belongs to the target class T.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge