Using k-medoids for distributed approximate similarity search with arbitrary distances

This paper presents GMASK, a general algorithm for distributed approximate similarity search that accepts any arbitrary distance function. GMASK requires a clustering algorithm that induces Voronoi regions in a dataset and returns a representative element for each region. Then, it creates a multilevel indexing structure suitable for large datasets with high dimensionality and sparsity, usually stored in distributed systems. Many similarity search algorithms rely on $k$-means, typically associated with the Euclidean distance, which is inappropriate for specific problems. Instead, in this work we implement GMASK using $k$-medoids to make it compatible with any distance and a wider range of problems. Experimental results verify the applicability of this method with real datasets, improving the performance of alternative algorithms for approximate similarity search. In addition, results confirm existing intuitions regarding the advantages of using certain instances of the Minkowski distance in high-dimensional datasets.

Unconventional application of k-means for distributed approximate similarity search

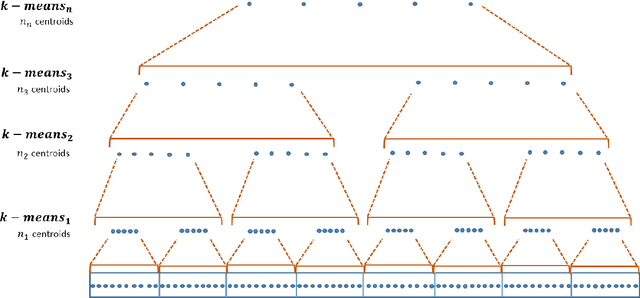
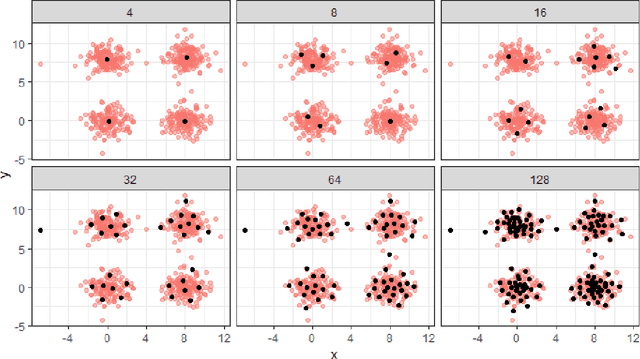
Similarity search based on a distance function in metric spaces is a fundamental problem for many applications. Queries for similar objects lead to the well-known machine learning task of nearest-neighbours identification. Many data indexing strategies, collectively known as Metric Access Methods (MAM), have been proposed to speed up queries for similar elements in this context. Moreover, since exact approaches to solve similarity queries can be complex and time-consuming, alternative options have appeared to reduce query execution time, such as returning approximate results or resorting to distributed computing platforms. In this paper, we introduce MASK (Multilevel Approximate Similarity search with $k$-means), an unconventional application of the $k$-means algorithm as the foundation of a multilevel index structure for approximate similarity search, suitable for metric spaces. We show that inherent properties of $k$-means, like representing high-density data areas with fewer prototypes, can be leveraged for this purpose. An implementation of this new indexing method is evaluated, using a synthetic dataset and a real-world dataset in a high-dimensional and high-sparsity space. Results are promising and underpin the applicability of this novel indexing method in multiple domains.