A Perspective on Neural Capacity Estimation: Viability and Reliability

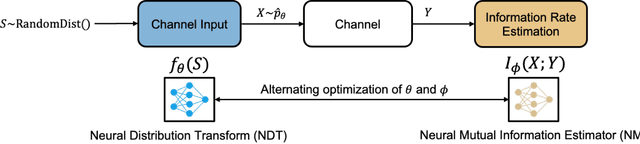
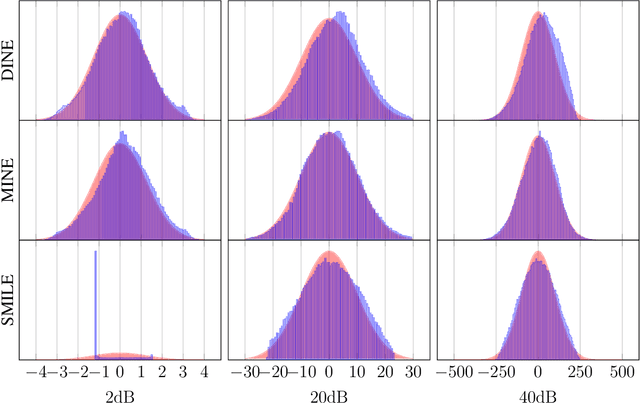
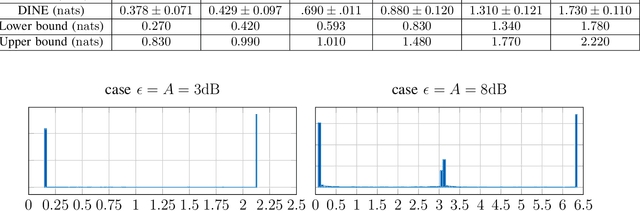
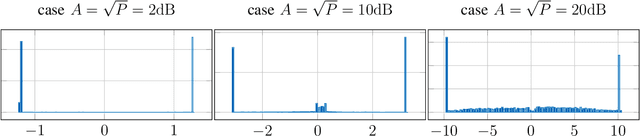
Recently, several methods have been proposed for estimating the mutual information from sample data using deep neural networks and without the knowledge of closed-form distribution of the data. This class of estimators is referred to as neural mutual information estimators (NMIE). In this paper, we investigate the performance of different NMIE proposed in the literature when applied to the capacity estimation problem. In particular, we study the performance of mutual information neural estimator (MINE), smoothed mutual information lower-bound estimator (SMILE), and directed information neural estimator (DINE). For the NMIE above, capacity estimation relies on two deep neural networks (DNN): (i) one DNN generates samples from a distribution that is learned, and (ii) a DNN to estimate the MI between the channel input and the channel output. We benchmark these NMIE in three scenarios: (i) AWGN channel capacity estimation and (ii) channels with unknown capacity and continuous inputs i.e., optical intensity and peak-power constrained AWGN channel (iii) channels with unknown capacity and a discrete number of mass points i.e., Poisson channel. Additionally, we also (iv) consider the extension to the MAC capacity problem by considering the AWGN and optical MAC models.

Neural Capacity Estimators: How Reliable Are They?

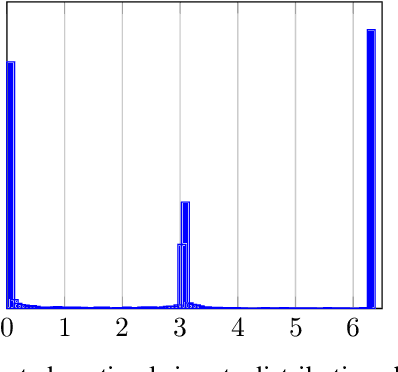
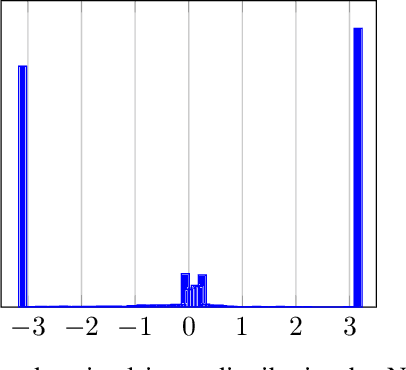
Recently, several methods have been proposed for estimating the mutual information from sample data using deep neural networks and without the knowing closed form distribution of the data. This class of estimators is referred to as neural mutual information estimators. Although very promising, such techniques have yet to be rigorously bench-marked so as to establish their efficacy, ease of implementation, and stability for capacity estimation which is joint maximization frame-work. In this paper, we compare the different techniques proposed in the literature for estimating capacity and provide a practitioner perspective on their effectiveness. In particular, we study the performance of mutual information neural estimator (MINE), smoothed mutual information lower-bound estimator (SMILE), and directed information neural estimator (DINE) and provide insights on InfoNCE. We evaluated these algorithms in terms of their ability to learn the input distributions that are capacity approaching for the AWGN channel, the optical intensity channel, and peak power-constrained AWGN channel. For both scenarios, we provide insightful comments on various aspects of the training process, such as stability, sensitivity to initialization.