Differentiable and Stable Long-Range Tracking of Multiple Posterior Modes

Particle filters flexibly represent multiple posterior modes nonparametrically, via a collection of weighted samples, but have classically been applied to tracking problems with known dynamics and observation likelihoods. Such generative models may be inaccurate or unavailable for high-dimensional observations like images. We instead leverage training data to discriminatively learn particle-based representations of uncertainty in latent object states, conditioned on arbitrary observations via deep neural network encoders. While prior discriminative particle filters have used heuristic relaxations of discrete particle resampling, or biased learning by truncating gradients at resampling steps, we achieve unbiased and low-variance gradient estimates by representing posteriors as continuous mixture densities. Our theory and experiments expose dramatic failures of existing reparameterization-based estimators for mixture gradients, an issue we address via an importance-sampling gradient estimator. Unlike standard recurrent neural networks, our mixture density particle filter represents multimodal uncertainty in continuous latent states, improving accuracy and robustness. On a range of challenging tracking and robot localization problems, our approach achieves dramatic improvements in accuracy, while also showing much greater stability across multiple training runs.

The Nonparametric Metadata Dependent Relational Model

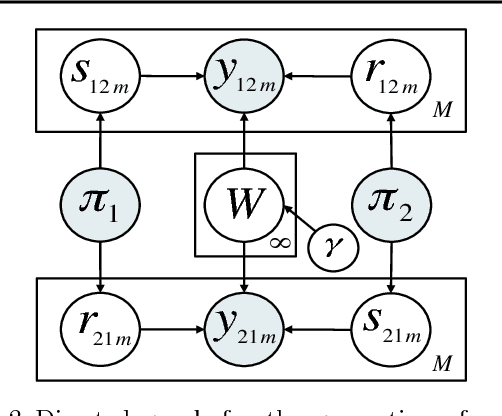
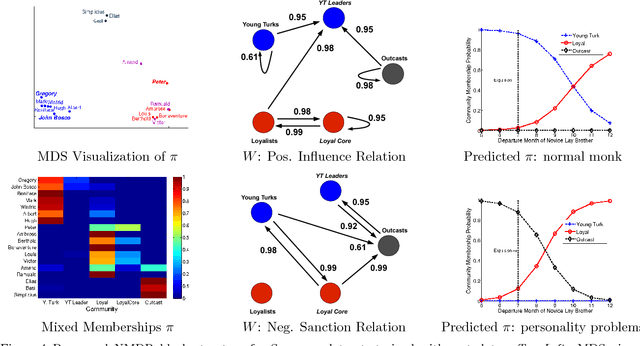
We introduce the nonparametric metadata dependent relational (NMDR) model, a Bayesian nonparametric stochastic block model for network data. The NMDR allows the entities associated with each node to have mixed membership in an unbounded collection of latent communities. Learned regression models allow these memberships to depend on, and be predicted from, arbitrary node metadata. We develop efficient MCMC algorithms for learning NMDR models from partially observed node relationships. Retrospective MCMC methods allow our sampler to work directly with the infinite stick-breaking representation of the NMDR, avoiding the need for finite truncations. Our results demonstrate recovery of useful latent communities from real-world social and ecological networks, and the usefulness of metadata in link prediction tasks.