On the Sample Complexity of Two-Layer Networks: Lipschitz vs. Element-Wise Lipschitz Activation

We investigate the sample complexity of bounded two-layer neural networks using different activation functions. In particular, we consider the class \[ \mathcal{H} = \left\{\textbf{x}\mapsto \langle \textbf{v}, \sigma \circ W\textbf{x} + \textbf{b} \rangle : \textbf{b}\in\mathbb{R}^d, W \in \mathbb{R}^{T\times d}, \textbf{v} \in \mathbb{R}^{T}\right\} \] where the spectral norm of $W$ and $\textbf{v}$ is bounded by $O(1)$, the Frobenius norm of $W$ is bounded from its initialization by $R > 0$, and $\sigma$ is a Lipschitz activation function. We prove that if $\sigma$ is element-wise, then the sample complexity of $\mathcal{H}$ is width independent and that this complexity is tight. Moreover, we show that the element-wise property of $\sigma$ is essential for width-independent bound, in the sense that there exist non-element-wise activation functions whose sample complexity is provably width-dependent. For the upper bound, we use the recent approach for norm-based bounds named Approximate Description Length (ADL) by arXiv:1910.05697. We further develop new techniques and tools for this approach, that will hopefully inspire future works.

An Exact Poly-Time Membership-Queries Algorithm for Extraction a three-Layer ReLU Network

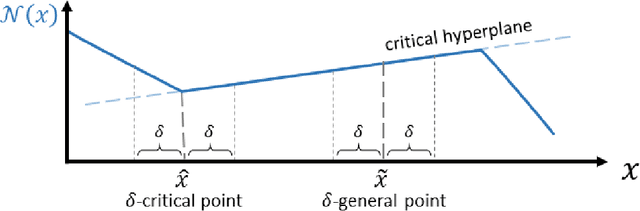
As machine learning increasingly becomes more prevalent in our everyday life, many organizations offer neural-networks based services as a black-box. The reasons for hiding a learning model may vary: e.g., preventing copying of its behavior or keeping back an adversarial from reverse-engineering its mechanism and revealing sensitive information about its training data. However, even as a black-box, some information can still be discovered by specific queries. In this work, we show a polynomial-time algorithm that uses a polynomial number of queries to mimic precisely the behavior of a three-layer neural network that uses ReLU activation.

Generalization Bounds for Neural Networks via Approximate Description Length

We investigate the sample complexity of networks with bounds on the magnitude of its weights. In particular, we consider the class \[ H=\left\{W_t\circ\rho\circ \ldots\circ\rho\circ W_{1} :W_1,\ldots,W_{t-1}\in M_{d, d}, W_t\in M_{1,d}\right\} \] where the spectral norm of each $W_i$ is bounded by $O(1)$, the Frobenius norm is bounded by $R$, and $\rho$ is the sigmoid function $\frac{e^x}{1+e^x}$ or the smoothened ReLU function $ \ln (1+e^x)$. We show that for any depth $t$, if the inputs are in $[-1,1]^d$, the sample complexity of $H$ is $\tilde O\left(\frac{dR^2}{\epsilon^2}\right)$. This bound is optimal up to log-factors, and substantially improves over the previous state of the art of $\tilde O\left(\frac{d^2R^2}{\epsilon^2}\right)$. We furthermore show that this bound remains valid if instead of considering the magnitude of the $W_i$'s, we consider the magnitude of $W_i - W_i^0$, where $W_i^0$ are some reference matrices, with spectral norm of $O(1)$. By taking the $W_i^0$ to be the matrices at the onset of the training process, we get sample complexity bounds that are sub-linear in the number of parameters, in many typical regimes of parameters. To establish our results we develop a new technique to analyze the sample complexity of families $H$ of predictors. We start by defining a new notion of a randomized approximate description of functions $f:X\to\mathbb{R}^d$. We then show that if there is a way to approximately describe functions in a class $H$ using $d$ bits, then $d/\epsilon^2$ examples suffices to guarantee uniform convergence. Namely, that the empirical loss of all the functions in the class is $\epsilon$-close to the true loss. Finally, we develop a set of tools for calculating the approximate description length of classes of functions that can be presented as a composition of linear function classes and non-linear functions.