Delaram Kahrobaei
Eidolon: A Practical Post-Quantum Signature Scheme Based on k-Colorability in the Age of Graph Neural Networks
Feb 02, 2026Abstract:We propose Eidolon, a practical post-quantum signature scheme based on the NP-complete k-colorability problem. Our construction generalizes the Goldreich-Micali-Wigderson zero-knowledge protocol to arbitrary k >= 3, applies the Fiat-Shamir transform, and uses Merkle-tree commitments to compress signatures from O(tn) to O(t log n). Crucially, we generate hard instances via planted "quiet" colorings that preserve the statistical profile of random graphs. We present the first empirical security analysis of such a scheme against both classical solvers (ILP, DSatur) and a custom graph neural network (GNN) attacker. Experiments show that for n >= 60, neither approach recovers the secret coloring, demonstrating that well-engineered k-coloring instances can resist modern cryptanalysis, including machine learning. This revives combinatorial hardness as a credible foundation for post-quantum signatures.
Solving the Conjugacy Decision Problem via Machine Learning
Feb 21, 2018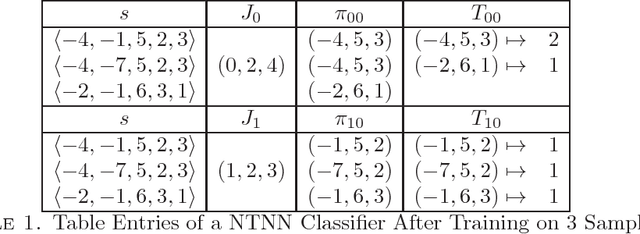
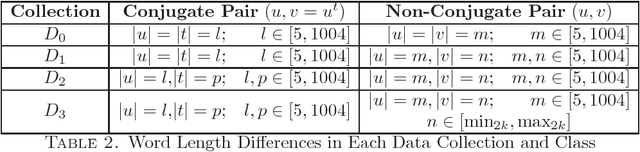


Abstract:Machine learning and pattern recognition techniques have been successfully applied to algorithmic problems in free groups. In this paper, we seek to extend these techniques to finitely presented non-free groups, with a particular emphasis on polycyclic and metabelian groups that are of interest to non-commutative cryptography. As a prototypical example, we utilize supervised learning methods to construct classifiers that can solve the conjugacy decision problem, i.e., determine whether or not a pair of elements from a specified group are conjugate. The accuracies of classifiers created using decision trees, random forests, and N-tuple neural network models are evaluated for several non-free groups. The very high accuracy of these classifiers suggests an underlying mathematical relationship with respect to conjugacy in the tested groups.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge