Debasmita Samaddar
Loss Landscape Engineering via Data Regulation on PINNs
May 16, 2022
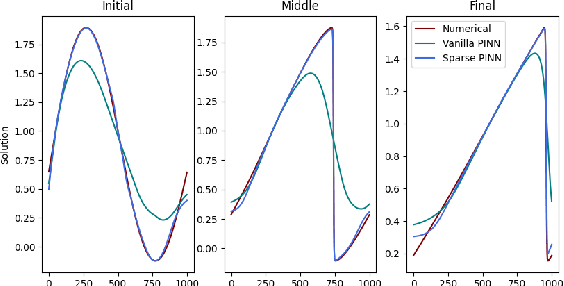


Abstract:Physics-Informed Neural Networks have shown unique utility in parameterising the solution of a well-defined partial differential equation using automatic differentiation and residual losses. Though they provide theoretical guarantees of convergence, in practice the required training regimes tend to be exacting and demanding. Through the course of this paper, we take a deep dive into understanding the loss landscapes associated with a PINN and how that offers some insight as to why PINNs are fundamentally hard to optimise for. We demonstrate how PINNs can be forced to converge better towards the solution, by way of feeding in sparse or coarse data as a regulator. The data regulates and morphs the topology of the loss landscape associated with the PINN to make it easily traversable for the minimiser. Data regulation of PINNs helps ease the optimisation required for convergence by invoking a hybrid unsupervised-supervised training approach, where the labelled data pushes the network towards the vicinity of the solution, and the unlabelled regime fine-tunes it to the solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge