Online Data Collection for Efficient Semiparametric Inference

While many works have studied statistical data fusion, they typically assume that the various datasets are given in advance. However, in practice, estimation requires difficult data collection decisions like determining the available data sources, their costs, and how many samples to collect from each source. Moreover, this process is often sequential because the data collected at a given time can improve collection decisions in the future. In our setup, given access to multiple data sources and budget constraints, the agent must sequentially decide which data source to query to efficiently estimate a target parameter. We formalize this task using Online Moment Selection, a semiparametric framework that applies to any parameter identified by a set of moment conditions. Interestingly, the optimal budget allocation depends on the (unknown) true parameters. We present two online data collection policies, Explore-then-Commit and Explore-then-Greedy, that use the parameter estimates at a given time to optimally allocate the remaining budget in the future steps. We prove that both policies achieve zero regret (assessed by asymptotic MSE) relative to an oracle policy. We empirically validate our methods on both synthetic and real-world causal effect estimation tasks, demonstrating that the online data collection policies outperform their fixed counterparts.

Local Causal Discovery for Estimating Causal Effects

Even when the causal graph underlying our data is unknown, we can use observational data to narrow down the possible values that an average treatment effect (ATE) can take by (1) identifying the graph up to a Markov equivalence class; and (2) estimating that ATE for each graph in the class. While the PC algorithm can identify this class under strong faithfulness assumptions, it can be computationally prohibitive. Fortunately, only the local graph structure around the treatment is required to identify the set of possible ATE values, a fact exploited by local discovery algorithms to improve computational efficiency. In this paper, we introduce Local Discovery using Eager Collider Checks (LDECC), a new local causal discovery algorithm that leverages unshielded colliders to orient the treatment's parents differently from existing methods. We show that there exist graphs where LDECC exponentially outperforms existing local discovery algorithms and vice versa. Moreover, we show that LDECC and existing algorithms rely on different faithfulness assumptions, leveraging this insight to weaken the assumptions for identifying the set of possible ATE values.

Efficient Online Estimation of Causal Effects by Deciding What to Observe

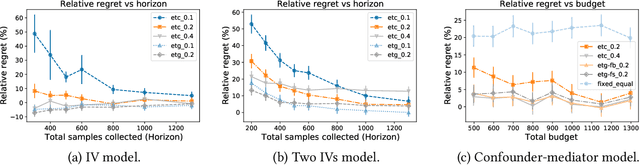
Researchers often face data fusion problems, where multiple data sources are available, each capturing a distinct subset of variables. While problem formulations typically take the data as given, in practice, data acquisition can be an ongoing process. In this paper, we aim to estimate any functional of a probabilistic model (e.g., a causal effect) as efficiently as possible, by deciding, at each time, which data source to query. We propose online moment selection (OMS), a framework in which structural assumptions are encoded as moment conditions. The optimal action at each step depends, in part, on the very moments that identify the functional of interest. Our algorithms balance exploration with choosing the best action as suggested by current estimates of the moments. We propose two selection strategies: (1) explore-then-commit (OMS-ETC) and (2) explore-then-greedy (OMS-ETG), proving that both achieve zero asymptotic regret as assessed by MSE. We instantiate our setup for average treatment effect estimation, where structural assumptions are given by a causal graph and data sources may include subsets of mediators, confounders, and instrumental variables.

Estimating Treatment Effects with Observed Confounders and Mediators

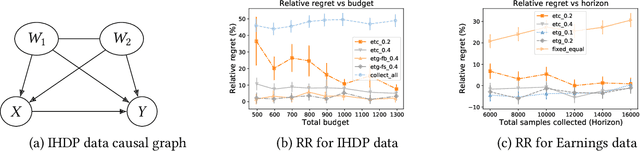
Given a causal graph, the do-calculus can express treatment effects as functionals of the observational joint distribution that can be estimated empirically. Sometimes the do-calculus identifies multiple valid formulae, prompting us to compare the statistical properties of the corresponding estimators. For example, the backdoor formula applies when all confounders are observed and the frontdoor formula applies when an observed mediator transmits the causal effect. In this paper, we investigate the over-identified scenario where both confounders and mediators are observed, rendering both estimators valid. Addressing the linear Gaussian causal model, we derive the finite-sample variance for both estimators and demonstrate that either estimator can dominate the other by an unbounded constant factor depending on the model parameters. Next, we derive an optimal estimator, which leverages all observed variables to strictly outperform the backdoor and frontdoor estimators. We also present a procedure for combining two datasets, with confounders observed in one and mediators in the other. Finally, we evaluate our methods on both simulated data and the IHDP and JTPA datasets.