Random Sparse Lifts: Construction, Analysis and Convergence of finite sparse networks

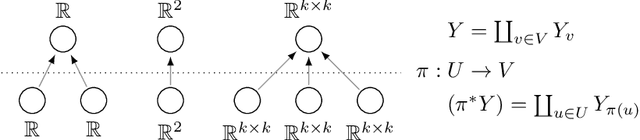
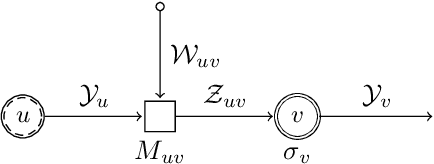
We present a framework to define a large class of neural networks for which, by construction, training by gradient flow provably reaches arbitrarily low loss when the number of parameters grows. Distinct from the fixed-space global optimality of non-convex optimization, this new form of convergence, and the techniques introduced to prove such convergence, pave the way for a usable deep learning convergence theory in the near future, without overparameterization assumptions relating the number of parameters and training samples. We define these architectures from a simple computation graph and a mechanism to lift it, thus increasing the number of parameters, generalizing the idea of increasing the widths of multi-layer perceptrons. We show that architectures similar to most common deep learning models are present in this class, obtained by sparsifying the weight tensors of usual architectures at initialization. Leveraging tools of algebraic topology and random graph theory, we use the computation graph's geometry to propagate properties guaranteeing convergence to any precision for these large sparse models.

Convergence beyond the over-parameterized regime using Rayleigh quotients

In this paper, we present a new strategy to prove the convergence of deep learning architectures to a zero training (or even testing) loss by gradient flow. Our analysis is centered on the notion of Rayleigh quotients in order to prove Kurdyka-{\L}ojasiewicz inequalities for a broader set of neural network architectures and loss functions. We show that Rayleigh quotients provide a unified view for several convergence analysis techniques in the literature. Our strategy produces a proof of convergence for various examples of parametric learning. In particular, our analysis does not require the number of parameters to tend to infinity, nor the number of samples to be finite, thus extending to test loss minimization and beyond the over-parameterized regime.