RL unknotter, hard unknots and unknotting number

We develop a reinforcement learning pipeline for simplifying knot diagrams. A trained agent learns move proposals and a value heuristic for navigating Reidemeister moves. The pipeline applies to arbitrary knots and links; we test it on ``very hard'' unknot diagrams and, using diagram inflation, on $4_1\#9_{10}$ where we recover the recently established and surprising upper bound of three for the unknotting number.

Big data comparison of quantum invariants

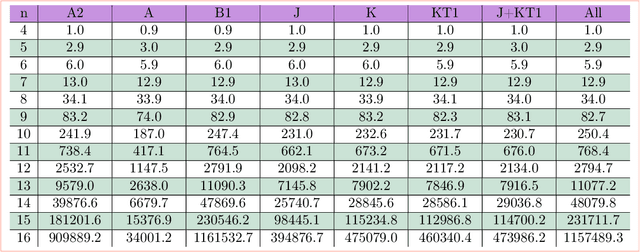
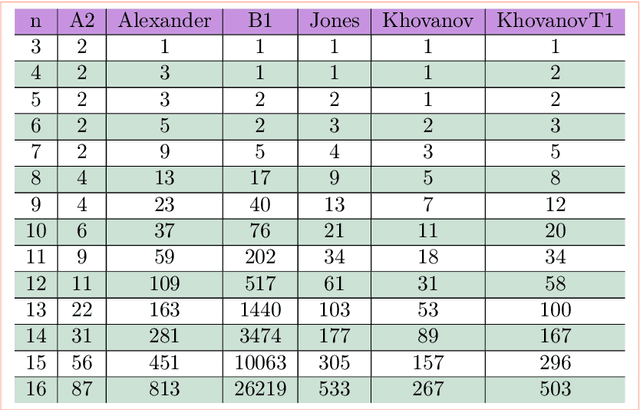
We apply big data techniques, including exploratory and topological data analysis, to investigate quantum invariants. More precisely, our study explores the Jones polynomial's structural properties and contrasts its behavior under four principal methods of enhancement: coloring, rank increase, categorification, and leaving the realm of Lie algebras.

Big data approach to Kazhdan-Lusztig polynomials

We investigate the structure of Kazhdan-Lusztig polynomials of the symmetric group by leveraging computational approaches from big data, including exploratory and topological data analysis, applied to the polynomials for symmetric groups of up to 11 strands.

Equivariant neural networks and piecewise linear representation theory

Equivariant neural networks are neural networks with symmetry. Motivated by the theory of group representations, we decompose the layers of an equivariant neural network into simple representations. The nonlinear activation functions lead to interesting nonlinear equivariant maps between simple representations. For example, the rectified linear unit (ReLU) gives rise to piecewise linear maps. We show that these considerations lead to a filtration of equivariant neural networks, generalizing Fourier series. This observation might provide a useful tool for interpreting equivariant neural networks.